GRMS一维河网模型

• 0. 前言
• 1. 控制方程
• 2. 数值格式
  • 2.1. HLL 格式的近似 Riemann 解
  • 2.2. Riemann 状态的非负重构
  • 2.3. 源项处理
  • 2.4 边界条件与干河床处理
  • 2.5 时间步长
• 3. 汊点
  • 3.1. 汊点约束方程
  • 3.2. 汊点水位迭代法
• 参考文献

0. 前言

​GRMS 一维河网模型采用有限体积方法求解 Saint-Venant（圣维南）方程组，有限体积方法基于积分格式，求解计算过程能够保证守恒性。方程组求解过程中采用 Hancock 预测-校正两步保证时间二阶精度，采用 MUSCL 线性插值保证空间二阶精度，通量计算采用 HLL 近似 Riemann 解。模型具有良好的激波捕获能力，能够模拟溃坝波以及复杂地形条件下的水流运动过程，对临界流、亚临界流、超临界流等各种流态转变过程均具有良好的模拟效果。

1. 控制方程

​描述天然河网一维浅水流动的 Saint-Venant 方程组的向量形式如下：

$$\pmb{D}\frac{\partial \pmb{U}}{\partial t} + \frac{\partial \pmb{F}}{\partial x} = \pmb{S} \tag{1}$$ 其中$\pmb{U}$为变量，$\pmb{F}$为通量，$\pmb{S}$为源项，其表达式如下：

$$\pmb{D} = \begin{bmatrix}B&0 \\0&1\end{bmatrix}，\pmb{U} = \begin{bmatrix}Z\\ Q\end{bmatrix}，\pmb{F}(\pmb{U}) = \begin{bmatrix}f1\\ f2\end{bmatrix}=\begin{bmatrix}Q\\ \frac{Q^2}{A}\end{bmatrix}，\pmb{S} = \begin{bmatrix}q\\ -gA\frac{\partial Z}{\partial x}-gAS_f\end{bmatrix} \tag{2}$$ 式中: $B$ 为水面宽度（m）；$Z$ 为水位（m）；$Q$ 为流量（$\text{m}^3/\text{s}$）；$A$ 为过水断面面积（$\text{m}^2$）；$f1$和$f2$分别代表向量$\pmb{F}(\pmb{U})$的两个分量；$q$为河道侧向入流（$\text{m}^2/\text{s}$）；$g$为重力加速度（$\text{m}/\text{s}^2$）；$t$为时间（s）；$s_f$为沿程阻力损失，其表达式为$S_f=(n^2Q|Q|)/(A^2R^{4/3})$；$R$为水力半径（m）；$n$为曼宁糙率系数。

考虑到水面坡度变化一般情况下比河道底坡变化平缓，因此在源项部分采用水面坡度项代表压力项的影响，有利于数值格式的稳定。此外，采用该形式也能避免不当的底坡项离散方法平衡数值通量时带来的计算格式不守恒问题¹。

2. 数值格式

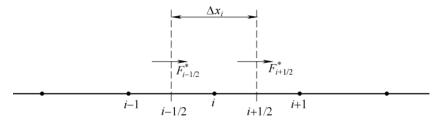
​GRMS 一维河网模型采用有限体积法离散控制方程，将水位、流量等水力要素信息存储在计算单元中心（即河道断面上）。将公式（1）在单元$i$上进行积分并根据 Gauss 定理离散后得：

$$\pmb{U}_{i}^{n+1}=\pmb{U}_{i}^{n}-\frac{\Delta t}{\Delta x_i}(\pmb{F}_{i+1/2}^{*}-\pmb{F}_{i-1/2}^{*})+\Delta t \pmb{D}_{i}^{-1} \pmb{S}_i \tag{3}$$ 式中：$\pmb{U}_i$为第$i$个单元变量的平均值；$\pmb{F}_{i+1/2}^{*}$，$\pmb{F}_{i-1/2}^{*}$分别为单元$i$左右两侧界面的数值通量（质量通量和动量通量）；$\Delta x_i$为第$i$个单元的长度（m）；$\Delta t$为时间步长（s）；$\pmb{S}_i$为第$i$个单元的源项。

​经过离散后，式（3）中的连续方程变为：

$$\pmb{Z}_{i}^{n+1}=\pmb{Z}_{i}^{n}-\frac{1}{B_i}\frac{\Delta t}{\Delta x_i}[(f_1)_{i+1/2}^{*}-(f_1)_{i-1/2}^{*}] \tag{4}$$ 可以看出，式中$Q$被通量$f_1$取代，根据Ying等²提出的理论，通量$f_1$可以保持很好的守恒特性。因此，采用通量$f_1$的值取代输出结果中的$Q$值，而由动量方程计算得到的$Q$值仅作为计算 Riemann 问题的中间变量。

2.1. HLL 格式的近似 Riemann 解

对界面通量采用 HLL（Harten, Lax, van Leer）格式近似 Riemann 解进行计算，通量求解过程如下： $$\pmb{F}^* = \left\{\begin{matrix} \pmb{F}(\pmb{U}_L) & \text{ if } s_{L}\geq0 \\ \pmb{F}_{LR}=\begin{bmatrix}\frac{B_{R}s_{R}f_{1}^{L}-B_{L}s_{L}f_{1}^{R}+B_{L}s_{L}B_{R}s_{R}(Z_{R}-Z_{L})}{B_{R}s_{R}-B_{L}s_{L}},\frac{s_{R}f_{2}^{L}-s_{L}f_{2}^{R}+s_{L}s_{R}(Q_{R}-Q_{L})}{s_{R}-s_{L}} \end{bmatrix}^{\text{T}} & \text{ if } s_{L}<0<s_{R} \\ \pmb{F}(\pmb{U}_{R}) & \text{ if } s_{R}\leq0 \end{matrix}\right. \tag{5}$$ 式中$s_L$和$s_R$为计算单元左右两侧的波速，当$s_L\geq0$和$s_R\leq0$时，计算单元界面处的通量值分别由其左右两侧单元的水力要素确定，当$s_L<0<s_R$时，计算单元界面处的通量值由 HLL 近似 Riemann 解给出。

2.2. Riemann 状态的非负重构

采用 MUSCL 线性重构方法对界面左右两侧的变量进行数值重构，其表达式为：

$$\pmb{U}_{i+1/2,L}=\pmb{U}_{i}+0.5\phi_{i}(\pmb{U}_{i}-\pmb{U}_{i-1}),\pmb{U}_{i+1/2,R}=\pmb{U}_{i+1}-0.5\phi_{i+1}(\pmb{U}_{i+1}-\pmb{U}_{i}) \tag{6}$$ 其中，$\phi$是限制器函数，采用 Minmod 限制器。同样的，界面左右两侧的水深重构为：

$$h_{i+1/2,L}=h_{i}+0.5\phi_{i}(h_{i}-h_{i-1}),h_{i+1/2,R}=h_{i+1}-0.5\phi_{i+1}(h_{i+1}-h_{i}) \tag{7}$$ 由于河道断面地形定义于控制体中心，基于均匀过渡假设，根据水深可求得界面两侧的$A$变量重构值（$A_{i+1/2,L}$、$A_{i+1/2,R}$）。又根据式（6）得到的界面两侧的流量，可求得界面两侧的流速$u_{i+1/2,L}$和$u_{i+1/2,R}$。界面两侧的河床底高程$(Z_b)_{i+1/2,L}$和$(Z_b)_{i+1/2,R}$由重构后的水位和水深计算得到，界面$i+1/2$处的河床底高程可按下式计算：

$$(Z_b)_{i+1/2}=\text {max}((Z_b)_{i+1/2,L},(Z_b)_{i+1/2,R}) \tag{8}$$ 基于$(Z_b)_{i+1/2}$，界面两侧的“恒正“水深定义为：

$$\stackrel{\sim}{h}_{i+1/2,L}=\text {max}(0,{Z}_{i+1/2,L}-(Z_b)_{i+1/2})\\ \stackrel{\sim}{h}_{i+1/2,R}=\text {max}(0,{Z}_{i+1/2,R}-(Z_b)_{i+1/2}) \tag{9}$$ 再由“恒正”水深可得到新的A变量的重构值（$\stackrel{\sim}A_{i+1/2,L}$、$\stackrel{\sim}A_{i+1/2,R}$），新的 Riemann 状态根据“恒正”水深构建为：

$$\stackrel{\sim}{Z}_{i+1/2,L}=\stackrel{\sim}h_{i+1/2,L}+(Z_b)_{i+1/2})， \stackrel{\sim}{Z}_{i+1/2,R}=\stackrel{\sim}h_{i+1/2,R}+(Z_b)_{i+1/2})\\ \stackrel{\sim}{Q}_{i+1/2,L}=u_{i+1/2,L}\stackrel{\sim}A_{i+1/2,L}， \stackrel{\sim}{Q}_{i+1/2,R}=u_{i+1/2,R}\stackrel{\sim}A_{i+1/2,R} \tag{10}$$ 当涉及到干湿界面时，如果干侧的河床底高程高于湿侧的河床底高程，可能会将湿侧的实际水位错误地替换为干侧的底高程，这会在单元中引入一个虚假的通量。考虑水体静止的情况，将会破坏这种静止状态。为了避免这种情况，Liang³首次引入了实际与虚假的水面高程之差来进一步修正重构后的 Riemann 状态：

$$\Delta Z=\text{max}(0,(Z_b)_{i+1/2}-Z_{i+1/2,L}) \tag{11}$$ 之后修正式（8）的床底高程和式（10）的水位 Riemann 状态：

$$(Z_b)_{i+1/2}\leftarrow(Z_b)_{i+1/2}-\Delta Z,\\ \stackrel{\sim}Z_{i+1/2,L}\leftarrow\stackrel{\sim}Z_{i+1/2,L}-\Delta Z, \stackrel{\sim}Z_{i+1/2,R}\leftarrow\stackrel{\sim}Z_{i+1/2,R}-\Delta Z \tag{12}$$ 由式（12）得到的河床底高程和水位，可计算出界面两侧新的A、B变量重构值，再加上式（10-12）修正后的 Riemann 状态，用于 HLL 近似 Riemann 解，可计算出$i+1/2$处的通量$\pmb{F}_{i+1/2}^{*}$。$i-1/2$处的通量$\pmb{F}_{i-1/2}^{*}$按上述过程同样可以求出。 为使数值解整体提高到二阶精度，同时维持数值解的稳定性，对时间步采用 Hancock 预测、校正两步格式： $$\pmb{U}_{i}^{n+1/2}=\pmb{U}_{i}^{n}-\frac{1}{2}\tfrac{\Delta t}{\Delta x_i}\pmb{D}_{i}^{-1}[\pmb{F}_{i+1/2}^{*}(\pmb{U}_{i+1/2}^{n})-\pmb{F}_{i-1/2}^{*}(\pmb{U}_{i-1/2}^{n})]\\ \pmb{U}_{i}^{n+1}=\pmb{U}_{i}^{n}-\tfrac{\Delta t}{\Delta x_i}\pmb{D}_{i}^{-1}[\pmb{F}_{i+1/2}^{*}(\pmb{U}_{i+1/2}^{n+1/2})-\pmb{F}_{i-1/2}^{*}(\pmb{U}_{i-1/2}^{n+1/2})]+\Delta {t}\pmb{D}_{i}^{-1}\pmb{S}_{i} \tag{13}$$ 其中$\pmb{U}_{i+1/2}^{n+1/2}$，$\pmb{U}_{i-1/2}^{n+1/2}$为计算的中间时刻变量。

2.3. 源项处理

​源项包括水面梯度项和摩阻项。摩阻项直接采用显格式处理。对于水面梯度项，为了保持数值解的光滑性，采用空间 MUSCL 数值重构后的水位来计算水面梯度，表达式如下：

$$\frac{\partial{Z}}{\partial{x_i}}=\frac{\overline{Z}_{i+1/2}-\overline{Z}_{i-1/2}}{\Delta{x_i}} \tag{14}$$ 其中，$\overline{Z}_{i+1/2}=(\stackrel{\sim}{Z}_{i+1/2,L}+\stackrel{\sim}{Z}_{i+1/2,R})/2$，$\overline{Z}_{i-1/2}=(\stackrel{\sim}{Z}_{i-1/2,L}+\stackrel{\sim}{Z}_{i-1/2,R})/2$。

2.4 边界条件与干河床处理

在边界外部引入一个镜像单元，其断面形状与相邻边界单元相同。对于水位边界，镜像单元的水位值等于给定的水位边界值，流量值与相邻的边界单元流量值相同；对于流量边界，镜像单元的流量值等于给定的流量边界值，水位值与相邻的边界单元水位值相同；对于水位-流量边界，镜像单元的水位、流量值分别等于给定的水位边界值和流量边界值；对于开边界，镜像单元的水位、流量值均与相邻边界单元的水位、流量值相同。

模型可能会对干河床情况进行模拟，通常可以在单元上定义一个足够小的水深，并使流速为零，这样干单元可按照求解湿单元的方法进行计算，不至于引起较大误差。

2.5 时间步长

时间步长受限于 CFL（Courant-Friedrichs-Lewy）稳定性条件：

$$N_{\text{CFL}}=\text{max}[\frac{\Delta t}{C\Delta x_i}(|u_i|+\sqrt{gA_i/B_i})]\leq1 \quad \text{ if } 1\leq i\leq N \tag{15}$$ 式中，$C$为 Courant 数，取值[0，1]；$N$为单元总数；其它变量同上。

3. 汊点

3.1. 汊点约束方程

​对于天然河网来说，河段的两个端点不是外边界点，就是汊点，在模型计算时，外边界的水力要素过程（水位、流量）已知，只需确定汊点处的水力要素值，即可进行河道下一时刻的模拟。实际上汊点连接关系通过连接河段边界节点变量实现河段间的水动力过程耦合，故汊点连接关系可以为各河段提供边界条件，即“汊点内边界条件”。汊点处水量守恒关系和能量守恒关系如下：

$$\sum_{i=1}^{M}Q_i=0 \tag{16}$$ $$Z_1=Z_2=...=Z_i=...=Z_M \tag{17}$$ 式中$M$为汊点处河段数，$Q_i$为河段流入汊点的流量（流入为正，流出为负），$Z_i$为河段$i$在汊点位置处的水位（均等于汊点水位）。 汊点连接条件除满足水量守恒和能量守恒两个基本关系外，同时满足明渠水流运动的特征线理论。沿着特征线$\text{C}_{\pm}:\text{d}x/\text{d}t=u\pm{c}$，有： $$\text{D}(u\pm{2c})/\text{D}t=-g(S_{f}-S_{0}) \tag{18}$$ 其中$u$为流速；$c$为波速；$S_{0}=-\text{d}Z_b/\text{d}x$为底床坡度。特征关系隐含了水位（或水深）与流量之间的关系，对于流入汊点的河段来讲，采用正特征线对应的特征关系，对于流出汊点的河段来讲，采用负特征线对应的特征关系。联解式（16-18），即可获得各连接河段在汊点处的流量值和水位值，该值作为河段的内边界条件进行下一时刻的计算。

3.2. 汊点水位迭代法

​汊点水位迭代法的核心思想是在汊点处给定水位边界条件，对每个河道单独求解，然后利用各河道求解结果对汊点水位边界条件进行校正，反复迭代直至汊点连接条件在误差允许范围内得到满足。根据陈永灿等⁴提出的汊点水位迭代法处理河网汊点连接条件，其表达式为：

$$Z_{j}^{2}-Z_{j}^{1}=\Delta Z_{j}=(\sum_{i=1}^{M_{in}}Q_{j,i}-\sum_{i=1}^{M_{out}}Q_{j,i})/(\alpha M\overline{B_j} \sqrt{gh_{j}}) \tag{19}$$ 式中：$Z_j^1$为汊点的预测水位值，$Z_j^2$为汊点校正后的水位值；$\Delta Z$为汊点水位校正量；$\sum_{i=1}^{M_{in}}Q_{j,i}$和$\sum_{i=1}^{M_{out}}Q_{j,i}$分别为汊点处断面流入汊点的总流量和流出汊点的总流量；$M$为汊点处河道数量；$\overline{B_j}$为汊点位置所有断面的水面宽度平均值；$h_j$为汊点水深；$\alpha$为大于1的计算参数，较大的$\alpha$值有利于计算的稳定，但代价是迭代次数增多，建议参考取值为1~2，实际计算中视收敛情况进行调整。

由式（19）可知，当预测的汊点水位偏低，导致流入汊点水量大于流出汊点水量时，汊点水位校正量大于0，使校正后的汊点水位升高，进而减少流入汊点的水量、增多流出汊点的水量；反之亦然。因此，上述的汊点水位迭代法是收敛的。

参考文献

¹. 张大伟, 权锦, 马建明, 等. 应用Godunov格式模拟复杂河网明渠水流运动[J]. 应用基础与工程科学学报,2015,23(6):1088-1096 ↩

². Ying X Y, Sam S Y, Wang F A P. Improved implementation of the HLL approximate Riemann solver for one-dimensional open channel flows[J]. Journal of Hydraulic Research,2008,46(1):21-34 ↩

³. Liang Q. Flood simulation using a well-balanced shallow flow model[J]. ASCE J Hydraul Eng,2010,136(9):69-75 ↩

⁴. 陈永灿, 王智勇, 朱德军, 刘昭伟, 等. 一维河网非恒定渐变流计算的汊点水位迭代法及其应用[J]. 水力发电学报,2010,29(4):140-147 ↩