GRMS一维河网水质模型
0. 前言
GRMS 一维河网水质模型基于采用有限体积方法求解 Saint-Venant(圣维南)方程组的一维河网模型,包括基础的对流扩散计算和考虑生物化学反应的富营养化计算。
1. 河网水质控制方程
描述单一河道污染物输移扩散的控制方程为一维对流扩散方程,具体形式如下:
∂ ( A C ) ∂ t + ∂ ( Q C ) ∂ x = ∂ ∂ x ( A E ∂ C ∂ x ) − S c + S (1)
\frac{\partial (AC)}{\partial t} + \frac{\partial (QC)}{\partial x} = \frac{\partial}{\partial x}(A E \frac{\partial C}{\partial x})-S_c+S
\tag{1}
∂ t ∂ ( A C ) + ∂ x ∂ ( QC ) = ∂ x ∂ ( A E ∂ x ∂ C ) − S c + S ( 1 ) Q Q Q m 3 / s \text{m}^3/\text{s} m 3 / s A A A m 2 \text{m}^2 m 2 C C C g / m 3 \text{g}/\text{m}^{3} g / m 3 E E E t t t s \text{s} s x x x m \text{m} m S c S_c S c S S S g / ( ms ) \text{g}/(\text{m}\text{s}) g / ( m s )
2. 数值求解
时间项离散为:
∂ ( A C ) ∂ t = A i n + 1 C i n + 1 − A i n C i n Δ t (2)
\frac{\partial(AC)}{\partial t} = \frac{A_{i}^{n+1} C_{i}^{n+1}-A_{i}^{n} C_{i}^{n}}{\Delta t}
\tag{2}
∂ t ∂ ( A C ) = Δ t A i n + 1 C i n + 1 − A i n C i n ( 2 ) n n n n + 1 n+1 n + 1 A i A_{i} A i i i i m 2 \text{m}^2 m 2 C i C_{i} C i i i i g / m 3 \text{g}/\text{m}^{3} g / m 3 Δ t \Delta t Δ t s \text{s} s
根据采用有限体积法离散的守恒格式圣维南方程的连续性方程,对流项离散为:
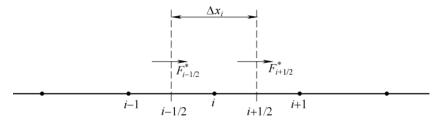
∂ ( Q C ) ∂ x = ( f 1 ) i + 1 / 2 ∗ C i + 1 / 2 ∗ − ( f 1 ) i − 1 / 2 ∗ C i − 1 / 2 ∗ Δ x i (3)
\frac{\partial (QC)}{\partial x} = \frac{(f_1)_{i+1/2}^{*} C_{i+1/2}^{*}-(f_1)_{i-1/2}^{*} C_{i-1/2}^{*}}{\Delta x_i}
\tag{3}
∂ x ∂ ( QC ) = Δ x i ( f 1 ) i + 1/2 ∗ C i + 1/2 ∗ − ( f 1 ) i − 1/2 ∗ C i − 1/2 ∗ ( 3 ) Δ x i \Delta x_i Δ x i ( f 1 ) i + 1 / 2 ∗ (f_1)_{i+1/2}^{*} ( f 1 ) i + 1/2 ∗ ( f 1 ) i − 1 / 2 ∗ (f_1)_{i-1/2}^{*} ( f 1 ) i − 1/2 ∗ i + 1 / 2 i+1/2 i + 1/2 i − 1 / 2 i-1/2 i − 1/2 m 3 / s \text{m}^3/\text{s} m 3 / s C i + 1 / 2 ∗ C_{i+1/2}^{*} C i + 1/2 ∗ C i − 1 / 2 ∗ C_{i-1/2}^{*} C i − 1/2 ∗ i + 1 / 2 i+1/2 i + 1/2 i − 1 / 2 i-1/2 i − 1/2 g / m 3 \text{g}/\text{m}^{3} g / m 3 C i + 1 / 2 ∗ = { C i n if ( f 1 ) i + 1 / 2 ∗ ≥ 0 C i + 1 n if ( f 1 ) i + 1 / 2 ∗ < 0 C i − 1 / 2 ∗ = { C i − 1 n if ( f 1 ) i − 1 / 2 ∗ ≥ 0 C i n if ( f 1 ) i − 1 / 2 ∗ < 0 (4)
C_{i+1/2}^* =
\left\{\begin{matrix}
C_{i}^n & \text{ if } (f_1)_{i+1/2}^*\geq0
\\ C_{i+1}^n & \text{ if } (f_1)_{i+1/2}^* < 0
\end{matrix}\right.
\\
C_{i-1/2}^* =
\left\{\begin{matrix}
C_{i-1}^n & \text{ if } (f_1)_{i-1/2}^*\geq0
\\ C_{i}^n & \text{ if } (f_1)_{i-1/2}^* < 0
\end{matrix}\right.
\tag{4}
C i + 1/2 ∗ = { C i n C i + 1 n if ( f 1 ) i + 1/2 ∗ ≥ 0 if ( f 1 ) i + 1/2 ∗ < 0 C i − 1/2 ∗ = { C i − 1 n C i n if ( f 1 ) i − 1/2 ∗ ≥ 0 if ( f 1 ) i − 1/2 ∗ < 0 ( 4 )
图1 一维中心格式有限体积法单元示意图
扩散项离散为:
∂ ∂ x ( A E ∂ C ∂ x ) = A i n + 1 E i n + 1 Δ x i ( C i + 1 n − C i n Δ x i + 1 / 2 − C i n − C i − 1 / 2 n Δ x i − 1 / 2 ) (5)
\frac{\partial}{\partial x}(A E \frac{\partial C}{\partial x}) = \frac{A_{i}^{n+1} E_{i}^{n+1}}{\Delta x_i}(\frac{C_{i+1}^{n}-C_{i}^{n}}{\Delta x_{i+1/2}}-\frac{C_{i}^{n}-C_{i-1/2}^{n}}{\Delta x_{i-1/2}})
\tag{5}
∂ x ∂ ( A E ∂ x ∂ C ) = Δ x i A i n + 1 E i n + 1 ( Δ x i + 1/2 C i + 1 n − C i n − Δ x i − 1/2 C i n − C i − 1/2 n ) ( 5 ) Δ x i + 1 / 2 \Delta x_{i+1/2} Δ x i + 1/2 i i i i + 1 i+1 i + 1 Δ x i − 1 / 2 \Delta x_{i-1/2} Δ x i − 1/2 i i i i − 1 i-1 i − 1 E i n + 1 = 0.07 h i n + 1 u ∗ E_{i}^{n+1}=0.07 h_{i}^{n+1} u^{*} E i n + 1 = 0.07 h i n + 1 u ∗ h i n + 1 h_{i}^{n+1} h i n + 1 i i i u ∗ u^* u ∗ m / s \text{m}/\text{s} m / s u ∗ = g R u^{*}=\sqrt{gR} u ∗ = g R g g g g / s 2 \text{g}/\text{s}^{2} g / s 2 R R R
3. 汊点
汊点可作为内边界条件为各河段提供污染物浓度边界,汊点处污染物质量守恒关系如下:
C c d n + 1 = ∑ j = 1 N i n Q j n + 1 C j n ∑ j = 1 N i n Q j n + 1 (6)
C_{cd}^{n+1}=\frac{\sum_{j=1}^{N_{in}} Q_{j}^{n+1} C_{j}^{n}}{\sum_{j=1}^{N_{in}} Q_{j}^{n+1}}
\tag{6}
C c d n + 1 = ∑ j = 1 N in Q j n + 1 ∑ j = 1 N in Q j n + 1 C j n ( 6 ) C c d n + 1 C_{cd}^{n+1} C c d n + 1 Q j n + 1 Q_{j}^{n+1} Q j n + 1 j j j C j n C_{j}^{n} C j n j j j N i n N_{in} N in
若汊点可蓄水,则汊点处污染物质量守恒关系如下:
V c d n + 1 C c d n + 1 − V c d n C c d n = Δ t ( ∑ j = 1 N i n Q j n + 1 C j n − ∑ k = 1 N o u t Q k n + 1 C c d n ) (7)
V_{cd}^{n+1} C_{cd}^{n+1}-V_{cd}^{n} C_{cd}^{n}=\Delta t(\sum_{j=1}^{N_{in}} Q_{j}^{n+1} C_{j}^{n}-\sum_{k=1}^{N_{out}} Q_{k}^{n+1} C_{cd}^{n})
\tag{7}
V c d n + 1 C c d n + 1 − V c d n C c d n = Δ t ( j = 1 ∑ N in Q j n + 1 C j n − k = 1 ∑ N o u t Q k n + 1 C c d n ) ( 7 ) V c d V_{cd} V c d m 3 \text{m}^3 m 3 C c d C_{cd} C c d Q j Q_{j} Q j j j j Q k Q_{k} Q k k k k C j C_{j} C j j j j N i n N_{in} N in N o u t N_{out} N o u t
4. 富营养化模型
4.1. 模型结构
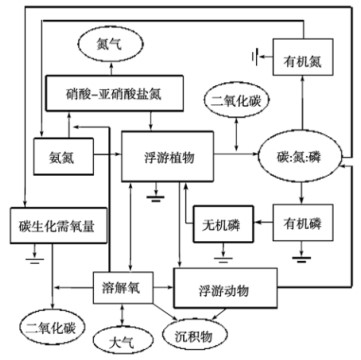
富营养化模型在美国环境保护局提出的水质模型程序 WASP(the Water Quality Analysis Simulation Program)中的 EUTRO 四个模块基础上,即 CBOD-DO 模块、浮游植物模块、氮循环模块、磷循环模块,构建溶解氧(DO)、碳生化需氧量(CBOD)、浮游植物(PHYT)、氨氮(N H 4 \text{N}\text{H}_4 N H 4 N \text{N} N N O 3 / N O 2 \text{N}\text{O}_3/\text{N}\text{O}_2 N O 3 / N O 2 N \text{N} N N H 4 \text{N}\text{H}_4 N H 4 N \text{N} N N O 3 / N O 2 \text{N}\text{O}_3/\text{N}\text{O}_2 N O 3 / N O 2 N \text{N} N C 1 、 C 2 、 C 3 、 C 4 、 C 5 、 C 6 、 C 7 、 C 8 C_1、C_2、C_3、C_4、C_5、C_6、C_7、C_8 C 1 、 C 2 、 C 3 、 C 4 、 C 5 、 C 6 、 C 7 、 C 8
图2 富营养化模型系统关系图
表1 富营养化模型变量消长因子
变量
生成项
消失项
C 1 C_1 C 1 复氧
浮游植、动物呼吸作用CBOD \text{CBOD} CBOD
C 2 C_2 C 2 浮游植物死亡
CBOD \text{CBOD} CBOD
C 3 C_3 C 3 浮游植物生长
浮游植物呼吸
C 4 C_4 C 4 浮游植物呼吸及死亡
浮游植物摄取
C 5 C_5 C 5 硝化作用
浮游植物摄取
C 6 C_6 C 6 浮游植物呼吸及死亡
有机氮矿化作用
C 7 C_7 C 7 浮游植物呼吸及死亡
浮游植物摄取
C 8 C_8 C 8 浮游植物呼吸及死亡
有机磷矿化作用
4.2. 富营养化变量方程
描述富营养化变量的方程形式如下:
∂ ( A C ) ∂ t + ∂ ( Q C ) ∂ x = ∂ ∂ x ( A E ∂ C ∂ x ) + S + A S k (8)
\frac{\partial (AC)}{\partial t} + \frac{\partial (QC)}{\partial x} = \frac{\partial}{\partial x}(A E \frac{\partial C}{\partial x})+S+AS_k
\tag{8}
∂ t ∂ ( A C ) + ∂ x ∂ ( QC ) = ∂ x ∂ ( A E ∂ x ∂ C ) + S + A S k ( 8 ) Q Q Q m 3 s − 1 \text{m}^3\text{s}^{-1} m 3 s − 1 A A A m 2 \text{m}^2 m 2 C C C g m − 3 \text{g}\text{m}^{-3} g m − 3 E E E t t t s \text{s} s x x x m \text{m} m S S S g m − 1 s − 1 \text{g}\text{m}^{-1}\text{s}^{-1} g m − 1 s − 1 S k S_k S k A S k AS_k A S k
4.3. 动力转换项的具体组成形式
4.3.1. 浮游植物模块
浮游植物在系统动力循环过程中起着重要作用,它影响到水环境中氮、磷、溶解氧等状态变量。其主要反应动力学方程如公式(2)~(4)所示。
S k 3 = C 3 ( G p − D p − V s 1 D ) (9)
S_{k3}=C_3(G_p-D_p-\frac{V_{s1}}{D})
\tag{9}
S k 3 = C 3 ( G p − D p − D V s 1 ) ( 9 ) G p G_p G p d − 1 \text{d}^{-1} d − 1 D p D_p D p d − 1 \text{d}^{-1} d − 1 V s 1 V_{s1} V s 1 d − 1 \text{d}^{-1} d − 1 D D D m \text{m} m
浮游植物生长率方程:
G p = K g max X r t X r i X r v (10)
G_p=K_{g\text{max}}X_{rt}X_{ri}X_{rv}
\tag{10}
G p = K g max X r t X r i X r v ( 10 ) K g max K_{g\text{max}} K g max d − 1 \text{d}^{-1} d − 1 X r t X_{rt} X r t X r i X_{ri} X r i X r v X_{rv} X r v
浮游植物呼吸与死亡率方程:
D p = K r ( t ) + K p + K g z (11)
D_p=K_{r}(t)+K_{p}+K_{gz}
\tag{11}
D p = K r ( t ) + K p + K g z ( 11 ) K r ( t ) K_{r}(t) K r ( t ) d − 1 \text{d}^{-1} d − 1 K p K_{p} K p d − 1 \text{d}^{-1} d − 1 K g z K_{gz} K g z d − 1 \text{d}^{-1} d − 1
4.3.2. 磷循环模块
可溶解的或可利用的 DIP 通过吸附-解吸机理与颗粒无机磷相互作用。浮游植物由于生长而吸收 DIP,因此 DIP 合成了浮游植物生物量。通过内源呼吸和非吞食性死亡,磷又从浮游植物生物体中返回到溶解和颗粒有机磷以及溶解无机磷。有机磷通过矿化能转化成溶解无机磷。其主要反应动力学方程如公式(5)~(6)所示:
有机磷:
S k 8 = D p C 3 A p c F o p − K 23 θ 23 T − 20 ( C 3 K m p c + C 3 ) C 8 − V s o p ( 1 − F d 2 ) D C 8 (12)
S_{k8}=D_{p}C_{3}A_{pc}F_{op}-K_{23}\theta_{23}^{T-20}(\frac{C_3}{K_{mpc}+C_3})C_8-\frac{V_{sop}(1-F_{d2})}{D}C_8
\tag{12}
S k 8 = D p C 3 A p c F o p − K 23 θ 23 T − 20 ( K m p c + C 3 C 3 ) C 8 − D V so p ( 1 − F d 2 ) C 8 ( 12 )
无机磷:
S k 7 = D p C 3 A p c ( 1 − F o p ) + K 23 θ 23 T − 20 ( C 3 K m p c + C 3 ) C 8 − G p C 3 A p c − V s i p ( 1 − F d 3 ) D C 7 (13)
S_{k7}=D_{p}C_{3}A_{pc}(1-F_{op})+K_{23}\theta_{23}^{T-20}(\frac{C_3}{K_{mpc}+C_3})C_8-G_{p}C_{3}A_{pc}-\frac{V_{sip}(1-F_{d3})}{D}C_7
\tag{13}
S k 7 = D p C 3 A p c ( 1 − F o p ) + K 23 θ 23 T − 20 ( K m p c + C 3 C 3 ) C 8 − G p C 3 A p c − D V s i p ( 1 − F d 3 ) C 7 ( 13 ) A p c A_{pc} A p c F o p F_{op} F o p K 23 K_{23} K 23 d − 1 \text{d}^{-1} d − 1 θ 23 \theta_{23} θ 23 T T T K m p c K_{mpc} K m p c mg/L \text{mg/L} mg/L V s o p V_{sop} V so p m/d \text{m/d} m/d F d 2 F_{d2} F d 2 V s i p V_{sip} V s i p m/d \text{m/d} m/d F d 3 F_{d3} F d 3
4.3.3. 氮循环模块
浮游植物生长吸收氨氮和硝酸-亚硝酸盐,并将其合成浮游植物生物量。吸收氮的速率是氮浓度的函数,而其浓度又与总的可利用无机氮有关。通过内源呼吸和非吞食性死亡,氮又从浮游植物生物量转化为溶解和颗粒有机氮以及氨。有机氮矿化为氨,其矿化速率又依赖于温度,而氨也可以转化成硝酸盐,其硝化速率也依赖于温度和氧气。硝酸盐在缺氧状况下,也可以转化成氮气,其反硝化速率是温度和氧气的函数。其反应动力学方程如公式(7)~(10)所示:
有机氮:
S k 6 = D p C 3 A n c F o n − K 45 θ 45 T − 20 ( C 3 K m p c + C 3 ) C 6 − V s o p ( 1 − F d 4 ) D C 6 (14)
S_{k6}=D_{p}C_{3}A_{nc}F_{on}-K_{45}\theta_{45}^{T-20}(\frac{C_3}{K_{mpc}+C_3})C_6-\frac{V_{sop}(1-F_{d4})}{D}C_6
\tag{14}
S k 6 = D p C 3 A n c F o n − K 45 θ 45 T − 20 ( K m p c + C 3 C 3 ) C 6 − D V so p ( 1 − F d 4 ) C 6 ( 14 )
氨氮:
S k 4 = D p C 3 A n c ( 1 − F o n ) + K 45 θ 45 T − 20 ( C 3 K m p c + C 3 ) C 6 − G p C 3 A n c P N H 3 − K 56 θ 56 T − 20 ( C 1 K n i t + C 1 ) C 4 (15)
S_{k4}=D_{p}C_{3}A_{nc}(1-F_{on})+K_{45}\theta_{45}^{T-20}(\frac{C_3}{K_{mpc}+C_3})C_6-G_{p}C_{3}A_{nc}P_{NH_3}-K_{56}\theta_{56}^{T-20}(\frac{C_1}{K_{nit}+C_1})C_4
\tag{15}
S k 4 = D p C 3 A n c ( 1 − F o n ) + K 45 θ 45 T − 20 ( K m p c + C 3 C 3 ) C 6 − G p C 3 A n c P N H 3 − K 56 θ 56 T − 20 ( K ni t + C 1 C 1 ) C 4 ( 15 )
P N H 3 = C 4 [ C 5 ( K m n + C 4 ) ( K m n + C 5 ) ] + C 4 [ K m n ( C 4 + C 5 ) ( K m n + C 5 ) ] (16)
P_{NH_3}=C_4[\frac{C_5}{(K_{mn}+C_4)(K_{mn}+C_5)}]+C_4[\frac{K_{mn}}{(C_4+C_5)(K_{mn}+C_5)}]
\tag{16}
P N H 3 = C 4 [ ( K mn + C 4 ) ( K mn + C 5 ) C 5 ] + C 4 [ ( C 4 + C 5 ) ( K mn + C 5 ) K mn ] ( 16 )
硝酸-亚硝酸盐氮:
S k 5 = K 56 θ 56 T − 20 ( C 1 K n i t + C 1 ) C 4 − G p C 3 A n c ( 1 − P N H 3 ) − K d θ D T − 20 ( K N O 3 K N O 3 + C 1 ) C 5 (17)
S_{k5}=K_{56}\theta_{56}^{T-20}(\frac{C_1}{K_{nit}+C_1})C_4-G_{p}C_{3}A_{nc}(1-P_{NH_3})-K_{d}\theta_{D}^{T-20}(\frac{K_{NO_3}}{K_{NO_3}+C_1})C_5
\tag{17}
S k 5 = K 56 θ 56 T − 20 ( K ni t + C 1 C 1 ) C 4 − G p C 3 A n c ( 1 − P N H 3 ) − K d θ D T − 20 ( K N O 3 + C 1 K N O 3 ) C 5 ( 17 ) A n c A_{nc} A n c F o n F_{on} F o n K 45 K_{45} K 45 d − 1 \text{d}^{-1} d − 1 θ 45 \theta_{45} θ 45 F d 4 F_{d4} F d 4 P N H 3 P_{NH_3} P N H 3 K n i t K_{nit} K ni t mg/L \text{mg/L} mg/L K d K_d K d d − 1 \text{d}^{-1} d − 1 θ D \theta_D θ D K N O 3 K_{NO_3} K N O 3 mg/L \text{mg/L} mg/L
4.3.4. CBOD-DO 子模块
溶解氧含量与其他状态变量相结合。溶解氧的来源有大气复氧和浮游植物的光合作用。溶解氧的消耗主要有浮游植动物的呼吸作用、水体中碳质物质的氧化、硝化作用。其反应动力学方程如公式(11)~(12)所示:
CBOD:
S k 2 = A o c D p C 3 − K o x θ o x T − 20 ( C 1 K B O D + C 1 ) C 2 − 5 4 32 14 K d θ D T − 20 ( K N O 3 K N O 3 + C 1 ) C 5 − V s o p ( 1 − F d 7 ) D C 2 (18)
S_{k2}=A_{oc}D_{p}C_{3}-K_{ox}\theta_{ox}^{T-20}(\frac{C_1}{K_{BOD}+C_1})C_2-\frac{5}{4}\frac{32}{14}K_{d}\theta_{D}^{T-20}(\frac{K_{NO_3}}{K_{NO_3}+C_1})C_5-\frac{V_{sop}(1-F_{d7})}{D}C_2
\tag{18}
S k 2 = A oc D p C 3 − K o x θ o x T − 20 ( K BO D + C 1 C 1 ) C 2 − 4 5 14 32 K d θ D T − 20 ( K N O 3 + C 1 K N O 3 ) C 5 − D V so p ( 1 − F d 7 ) C 2 ( 18 )
DO:
S k 1 = K 2 θ 2 T − 20 ( C s − C 1 ) + G p [ 32 12 + 48 14 14 12 ( 1 − P N H 3 ) ] C 3 − K o x θ o x T − 20 ( C 1 K B O D + C 1 ) C 2 − 64 14 K 56 θ 56 T − 20 ( C 1 K n i t + C 1 ) C 4 − 32 12 K r c θ R C T − 20 C 3 − O D θ O T − 20 (19)
S_{k1}=K_{2}\theta_{2}^{T-20}(C_s-C_1)+G_{p}[\frac{32}{12}+\frac{48}{14}\frac{14}{12}(1-P_{NH_3})]C{3}
\\-K_{ox}\theta_{ox}^{T-20}(\frac{C_1}{K_{BOD}+C_1})C_2-\frac{64}{14}K_{56}\theta_{56}^{T-20}(\frac{C_1}{K_{nit}+C_1})C_{4}-\frac{32}{12}K_{rc}\theta_{RC}^{T-20}C_{3}-\frac{O}{D}\theta_{O}^{T-20}
\tag{19}
S k 1 = K 2 θ 2 T − 20 ( C s − C 1 ) + G p [ 12 32 + 14 48 12 14 ( 1 − P N H 3 )] C 3 − K o x θ o x T − 20 ( K BO D + C 1 C 1 ) C 2 − 14 64 K 56 θ 56 T − 20 ( K ni t + C 1 C 1 ) C 4 − 12 32 K rc θ RC T − 20 C 3 − D O θ O T − 20 ( 19 )
CBOD 方程式中第一项为浮游植物死亡项,第二项为 CBOD 氧化项,第三项为反硝化作用项,第四项为含碳物沉降项;DO 方程式中第一项为大气复氧项,第二项为浮游植物生长项,第三项为 CBOD 氧化项,第四项为硝化作用项,第五项为浮游植、动物呼吸作用项,第六项为底泥耗氧项;A o c A_{oc} A oc K o x K_{ox} K o x CBOD \text{CBOD} CBOD d − 1 \text{d}^{-1} d − 1 θ o x \theta_{ox} θ o x K B O D K_{BOD} K BO D mg/L \text{mg/L} mg/L F d 7 F_{d7} F d 7 K 2 K_2 K 2 d − 1 \text{d}^{-1} d − 1 θ 2 \theta_2 θ 2 C s C_s C s mg/L \text{mg/L} mg/L O O O g / m 2 \text{g}/\text{m}^2 g / m 2 θ O \theta_O θ O