新安江模型

考虑降水和流域下垫面分布不均匀的影响，新安江模型的结构设计为分散性的，分为四个层次结构：蒸散发计算，产流计算，分水源计算和汇流计算。该模型按照三层蒸散发模式计算流域蒸散发，按蓄满产流概念计算降雨产生的总径流量，采用流域蓄水曲线考虑下垫面不均匀对产流面积变化的影响。在径流成分划分方面，对三水源情况，按“山坡水文学”产流理论用一个具有有限容积和测孔、底孔的自由水蓄水库把总径流划分成饱和地面径流、壤中水径流和地下水径流。在汇流计算方面，单元面积的地面径流汇流一般采用单位线法，壤中水径流和地下水径流的汇流则采用线性水库法。河网汇流一般采用分段连续演算的 Muskingum 法或滞时演算法。

新安江模型的流程图

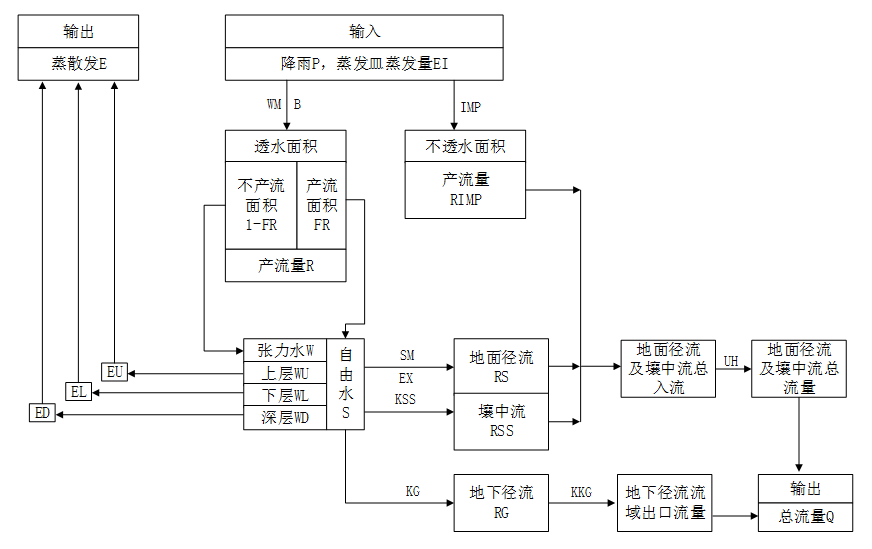
蒸散发计算
产流量计算
水源划分
坡地汇流计算
河网汇流计算
参数物理含义
参数独立性和敏感性

蒸散发计算

新安江三水源模型中的蒸散发计算采用的是三层蒸发计算模式，输入的是蒸发器实测水面蒸发和流域蒸散发能力的折算系数 $K$ ，模型的参数是上、下、深三层的蓄水容量 $WUM$ 、 $WLM$ 、 $WDM(WM=WUM+WLM+WDM)$ 和深层蒸散发系数 $C$ 。输出的是上、下、深各层的流域蒸散发量 $EU$ 、 $EL$ 和 $ED(E=EU+EL+ED)$ 。计算中包括三个时变参量，即各层土壤含水量 $WU$ 、 $WL$ 和 $WD(W=WU+WL+WD)$ 。以上的 $WM$ 、 $E$ 、 $W$ 分别表示总的流域蓄水容量、蒸散发量、土壤含水量。所用公式如下：

$\tag{1} 当 P-E+WU≥EP时\\则EU=EP，EL=0，ED=0$

$\tag{2} 当 P-E+WU<EP时\\则EU=P-E+WU$

$\tag{3} 当 WLC×WLM 时\\则EL=(EP-EU)×\frac{WL}{WLM}，ED=0$

$\tag{4} 当 WL<C×WLM 且WL≥C×（EP-EU)时\\则EL=C×(EP-EU)，ED=0$ `

$\tag{5} 当 WL<C×WLM 且WL<C×（EP-EU)时\\则EL=WL,ED=C×(EP-EU)-WL，ED=0$

以上公式中: $EP=K×EM$

产流量计算

产流量计算系根据蓄满产流理论得出的。所谓蓄满，是指包气带的含水量达到田间持水量。在土壤湿度未达到田间持水量时不产流，所有降雨都被土壤吸收，成为张力水。而当土壤湿度达到田间持水量后，所有降雨(减去同期蒸发)都产流。

一般说来，流域内各点的蓄水容量并不相同，新安江三水源模型把流域内各点的蓄水容量概化成如图所示的一条抛物线：

$\tag{1}\frac{f}{F}=1-(1-\frac{W'_m}{W'_{mm}})^B$ 式中： $W'_{mm}$ 为流域内最大的点蓄水容量； $W'_m$ 为流域内某一点的蓄水容量； $f$ 为蓄水容量 $≤W'_m$ 值时的流域面积； $F$ 为流域面积； $B$ 为抛物线指数。

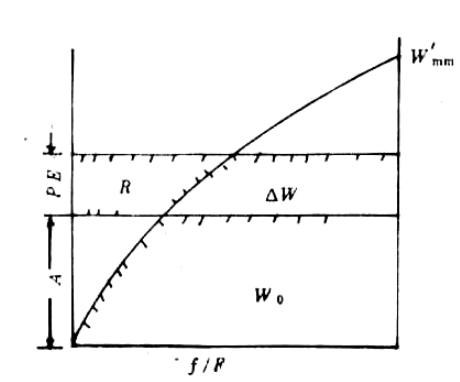
据此可求得流域平均蓄水容量为　　　　 $\tag{2}WM=\int_0^{W'_{mm}}(1-\frac{f}{F})dW'_m=\frac{W'_{mm}}{B+1})$ 与流域初始平均蓄水量 $W'_0$ 相应的纵坐标( $A$ )为　　　　 $\tag{3}A=W'_{mm}[1-(1-\frac{W_0}{WM})^\frac{1}{B+1})]$

当 $PE=P-E>0$ 时，则产流；否则不产流。产流时　　　　

$\tag{4}当PE+A<W'_{mm}时，则R=PE-WM+W_0+WM(1-\frac{PE+A}{W'_{mm}})^{1+B}$

$\tag{5}当PE+A≥W'_{mm}时，则R=PE-(WM-W_0）$

作产流计算时，模型的输入为 $PE$ ，参数包括流域平均蓄水容量 $WM$ 和抛物线指数 $B$ ；输出为流域产流量 $R$ 及流域时段末土壤平均蓄水量 $W$ 。

水源划分

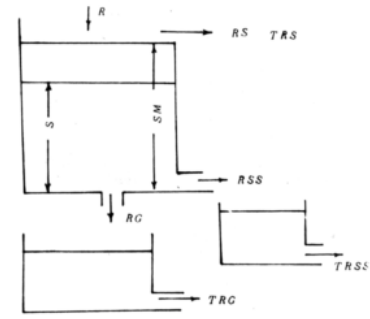
三水源新安江模型用自由水蓄水库的结构代替原先 $FC$ 的结构，以解决水源划分问题。按蓄满产流模型求出的产流量 $R$ 。先进入自由水蓄量 $S$ ，再划分水源，如下图所示。此水库有两个出口，一个底孔形成地下径流 $RG$ ，一个边孔形成壤中流 $RSS$ ，其出流规律均按线性水库出流。由于新安江模型考虑了产流面积 $FR$ 问题，所以这个自由水蓄水库只发生在产流面积上，其底宽 $FR$ 是变化的，产流量 $R$ 进入水库即在产流面积上，使得自由水蓄水库增加蓄水深，当自由水蓄水深 $S$ 超过其最大值 $SM$ 时，超过部分成为地面径流 $RS$ 。模型认为，蒸散发在张力水中消耗，自由水蓄水库的水量全部为径流。

图中： $S$ 为自由水蓄水库的蓄水深； $SM$ 为自由水蓄水库的蓄水容量； $FR$ 为产流面积。

底孔出流量 $RG$ 和边孔出流量 $RSS$ 分别进入各自的水库，并按线性水库的退水规律流出，分别成为地下水总入流 $TRG$ 和壤中流总入流 $TRSS$ 。并认为地面径流的坡地汇流时间可以忽略不计。所以地面径流 $RS$ 可认为与地面径流的总入流 $TRS$ 相同。

由于产流面积 $FR$ 上自由水的蓄水容量还不能认为是均匀分布的，即 $SM$ 为常数不太合适，要考虑 $SM$ 的面积分布。这实际上就是饱和坡面流的产流面积不断变化的问题。

模仿张力水分布不均匀的处理方式，把自由水蓄水能力在产流面积上的分布也用一条抛物线来表示，见下图。

$\tag{1} 即\frac{FS}{FR}=1-(1-\frac{SMF'}{SMMF})^{EX}$

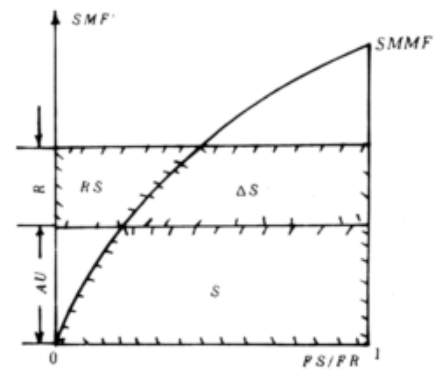
式中： $SMF'$ 为产流面积 $FR$ 上某一点的自由水容量； $SMMF$ 为产流面积 $FR$ 上最大一点的自由水蓄水容量； $FS$ 为自由水蓄水能力 $≤SMF'$ 值的流域面积； $FR$ 为产流面积； $EX$ 为流域自由水蓄水容量曲线的指数。

产流面积上的平均蓄水容量深 $SMF$ 为 $\tag{2} SMF=\frac{SMMF}{1+EX}$

在自由水蓄水容量曲线上 $S$ 相应的纵坐标 $AU$ 为 $\tag{3} AU=SMMF[1-(1-\frac{S}{SMF})^\frac{1}{1+EX}]$

式中： $S$ 为流域自由水蓄水容量曲线上的自由水在产流面积上的平均蓄水深； $AU$ 为 $S$ 对应的纵坐标。

显然， $SMMF$ 和 $SMF$ 都是产流面积 $FR$ 的函数，是无法确定的变量。这里假定 $SMMF$ 与产流面积 $FR$ 及全流域上最大一点的自由水蓄水容量 $SMF$ 的关系仍为抛物线分布 $\tag{4} FR=1-(1-\frac{SMMF}{SMF})^{EX}$

$\tag{5} 则　　　SMMF=[1-(1-FR)^\frac{1}{EX}]SMM\\SMM=SM(1+EX)$

流域的平均自由水容量 $SM$ 和抛物线指数 $EX$ 对于一个流域来说是固定的，属于模型率定的参数。已知 $SM$ 和 $EX$ ，就可以得到 $SMMF$ 。

已知上时段的产流面积 $FR0$ 和产流面积上的平均自由水深 $S0$ ，根据时段产流量 $R$ ，计算时段地面径流、壤中流、地下径流及本时段产流面积 $FR$ 和 $FR$ 上的平均自由水深 $S$ 的步骤是

$\tag{6} FR=R/PE\\S=S0·FR0/FR\\SMM=SM·(1+EX)\\SMMF=SMM·[1-(1-FR)^{1/EX}]\\SMF=SMMF/(1+EX)\\AU=SMMF[1-(1-\frac{S}{SMF})^\frac{1}{(1+EX)}]$

当 $PE+AU≥SMMF$ 时

$\tag{7} 则　　RS=FR(PE+S-SMF)\\RSS=SMF·KSS·FR\\RG=SMF·KG·FR\\S=SMF-(RSS+RG)/FR$

当 $0<PE+AU<SMMF$ 时

$\tag{8}则　　RS=FR·[PE-SMF+S+SMF(1-\frac{PE+AU}{SMMF})^{EX+1}]\\RSS=KSS·FR(PE+S-RS/FR)\\RG=KG·FR(PE+S-RS/FR)\\S=S+PE-(RS+RSS+RG)/FR$

式中： $KSS$ 和 $KG$ 分别为壤中流与地下径流的日出流系数。

坡地汇流计算

新安江三水源模型中把经过水源划分得到的地面径流 $RS$ 直接进入河网，成为地面径流对河网的总入流 $TRS$ 。壤中流 $RSS$ 流入壤中流水库，经过壤中流蓄水库的消退(壤中流水库的消退系数为 $KKSS$ )，成为壤中流对河网总入流 $TRSS$ 。地下径流 $RG$ 进入地下蓄水库，经过地下蓄水库的消退(地下蓄水库的消退系数为 $KKG$ )，成为地下水对河网的总入流( $TRG$ )。其计算公式为：

$\tag{1} TRS(t)=RS(t)·U$ $\tag{2} TRSS(t)=TRSS(t-1)·KKSS+RSS(t)·(1-KKSS)·U$ $\tag{3} TRG(t)=TRG(t-1)·KKG+RG(t)·(1-KKG)·U$ $\tag{4} TR(t)=TRS(t-1)+TRSS(t)+TRG(t)$

式中： $U$ 为单位转换系数，可将径流深转化为流量，即从 $mm$ 转化为 $m^3/s$ ， $U=F/3.6\Delta t$ ( $F$ 为流域面积； $\Delta t$ 为时段长)，为河网总入流( $m^3/s$ )。

河网汇流计算

新安江三水源模型中采用无因次单位线模拟水体从进入河槽到单元出口的河网汇流。在本流域或临近流域，找一个有资料的、面积与单元流域大体相近的流域，分析出地面径流单位线，就可作为初值应用。计算公式为

$\tag{1} Q(t)= \sum_{i=1}^{i=N}UH(i)×TR(t-i+1)$ 式中： $Q(t)$ 为单元出口处 $t$ 时刻的流量值； $UH$ 为无因次时段单位线； $N$ 为单位线的历时时段数。

由于单位线确定较为困难，经常采用滞后演算法进行河网汇流计算。即：

$\tag{2} Q(t)=CS×Q(t-1)+(1-CS)×TR(t-L)$ 流域汇流计算的输入是单元上的地面径流、壤中流、地下径流及计算开始时刻的单元面积上壤中流流量和地下径流流量值。输出为单元出口的流量过程。

参数物理含义

蒸散发参数（K、UM、LM、C）

K为蒸散发能力折算系数，是指流域蒸散发能力与实测水面蒸发值之比。此参数控制着总水量平衡，因此对水量计算是十分重要的。 UM为上层蓄水容量，它包括植物截留量。在植被与土壤比较发育的流域，约为 20mm；在植被与土壤颇差的流域，约为5~6mm。 LM为下层蓄水容量。可取 60~90mm。

C为深层蒸散发系数。它决定于深根植物占流域面积的比数，同时也与 UM + LM 的值有关，此值越大，深层蒸散发越困难。一般经验，在江南湿润地区 C 值约为 0.15~0.20，而在华北半湿润地区则在 0.09~0.12 左右。

产流量参数（WM、B、IM）

WM为流域蓄水容量，是流域干旱程度的指标。根据久旱以后下大雨的资料，如在雨前，可认为蓄水量为0，雨后可认为已蓄满，则此次洪水的总损失量就是WM，可从实测资料中求得。若无资料，则只能根据久旱后的几次降雨，用估计的方法求出。WM一般分为上层UM、下层LM和深层DM。在南方约为120mm，北方半湿润地区约为180mm。

B为蓄水容量曲线的方次。它反映流域上蓄水容量分布的不均匀性。一般经验，流域越大，各种地质地形配置越多样，B值也越大。在山丘区，很小面积（几平方公里）的B为0.1左右，中等面积（300平方公里以内）的B为0.2~0.3左右，较大面积（数千平方公里）的B值为0.3~0.4左右。但需说明，B值与UM有关，相互并不完全独立。同流域蓄水容量曲线，如WM加大，B就相应减少，反之亦然。

IM为不透水面积占全流域面积之比。如有详细地图，可以量出，但一般不可能，可找干旱期降小雨的资料来分析，这时有一很小洪水，完全是不透水面积上产生的。求出此洪水的径流系数，就是IM。

水源划分参数（SM、EX、KI、KG）

SM为流域平均自由水蓄水容量，本参数受降雨资料时段均化的影响，当用日为时段长时，一般流域的SM值约为10~50mm。当所取时段长较小时，SM要加大。这个参数对地面径流的多少起着决定性作用，因此很重要。

EX为自由水蓄水容量曲线指数，它表示自由水容量分布不均匀性。通常EX取值在1~1.5之间。

KI为自由水蓄水库对壤中流的出流系数，KG为自由水蓄水库对地下径流出流系数，这两个出流系数是并联的，其和代表着自由水出流的快慢。一般来说，KI + KG = 0.7，相当于从雨止到壤中流止的时间为3天。如果退水历时为2天，则KI + KG = 0.8。但有的流域退水历时远大于3天，表示深层壤中流起了作用，应由参数CI来处理。

参数独立性和敏感性

新安江模型的参数可分为如下 4 类:

1类，蒸散发计算，K，UM，LM,C;
2类，产流量计算，WM，B，IM;
3类，分水源计算，SM，EX，KG，KI;
4类，汇流计算，CI，CG，UH，KE，XE。

计算就是按这个顺序进行的。各类参数具有各自的作用和目标，因此相互之间独立性较好。而同类参数之间由于目标相同，相互之间的相关性就更大。

第1、2类之间。当参数B有变化时对产流量R的计算结果有影响，因此影响总水量平衡，也就影响第一类参数值的调试结果，但这种作用很小。 WM 不影响蒸散发计算，因此与第1类参数无关。但由于WM与B有关，因此间接产生一点影响。IM 本身作用不大，影响很小。
第2、3类之间。由于采用了蓄满产流概念，在分水源以前已把总产流量算好，所以第 3类参数完全不影响第 2 类参数。
第3、4 类之间。分水源计算结束后求得的是河网总入流。汇流计算只处理河网汇流问题，就与水源划分无关了。因此，第 3、4 类参数之间，性质上是完全独立的。但在优选参数时，都只能根据流量过程线，因此会有一定的相关性。但是可以利用高低水分段处理的办法来增强独立性。因为，高水控制地面径流，决定了参数SM，EX，KG+KI，UH低水控制地下径流，决定了参数KG/KI，CG。洪水尾部控制壤中流，决定了参数KG/KI，CI。如果分段采用目标函数，这些参数之间的独立性就可以显示出来。
第 1 类中，加大UM、LM与C的值就会加大计算E的值，因此在作水量平衡调试时就会减小K的值。但是，UM与LM都有一定的变化范围，所以这种影响是很有限的。至于C值，它只对干旱期有作用，可以从干旱期的资料中分析出来，独立性是好的。由于湿润地区很少用到深层蒸发，所以C 值并不敏感。但对半湿润地区，它是重要的。
第 2 类中，如果流域的张力水蓄水容量曲线不变，则WM愈大，B值就愈小，两者并不独立。但WM的变化范围不大，B值的变化范围也不大，B值并不敏感。WM也不敏感，它只代表蓄满的标准，并不影响蒸散发计算。但它有一个约束条件，即计算W值不能为负。当出现负值时，应加大WM，重新计算。
第 3 类参数是敏感和重要的，相互间的关系也比较复杂，要认真分析。 SM与EX之间是不独立的，其关系相当于WM与B的关系。但WM与B的关系可以根据降雨径流相关图求出，而SM与EX的关系则没有类似的办法可以求解，因此只能依靠优化检验的办法来分析。分析的办法如下:
先经验调试好全部参数值，然后把其它参数值固定不变，只变SM与EX，观察最优解落在哪。由于KG+KI已经固定，EX也已固定，所以SM就决定了地面径流的多少，KG/KI就决定了壤中流与地下水的多少。SM与KG/KI关系的分析，可以说明水源划分的解是否稳定，即在最优条件下，水源划分是否可能有较大的变化。
第4类中 CI的作用是弥补 KG + KI=0.7 的不足。它决定于洪水尾部退水的快慢，与别的条件无关，因此是比较独立的。但它对于整个过程的影响，远不如SM与KG/KI明显。 CG决定于地下水退水的快慢，也是比较独立的，用枯季资料很容易把它推求出来。 UH(或L及CS)决定于流量过程线的中高水部分，因此与第 3 类参数之间是比较独立的。但洪水过程线变化很快，用日模型是不够的，要取更小的时段长来作次洪模型。此外，UH还与KE，XE之间有相关性，当单元面积的汇流快一些，河网汇流就可以慢一些，相互有补偿作用。但对于降雨分布很不均匀的洪水，这两种汇流的作用是可以区别出来的。