坡面汇流模型

线性水库模型

线性水库是指水库的蓄水量与出流量之间的关系为线性函数。根据众多资料的分析表明，流域地下水的贮水结构近似为一个线性水库，下渗的净雨量为其入流量，经地下水库调节后的出流量就是地下径流的出流量。地下水线性水库满足蓄泄方程与水量平衡方程:

12(I1+I2)−12(Q1+Q2)=W2−W1Δt \frac{1}{2} (I_1 + I_2) - \frac{1}{2}(Q_1 + Q_2) = \frac{W_2 - W_1}{\Delta t}

W=KQ W = K Q

式中，I1,I2I_1, I_2时段初、末地下径流的入流量，m3/s；Q1,Q2Q_1, Q_2 时段初、末地下径流的出流量，m3/s；W1,W2W_1, W_2 时段初、末地下水蓄量，m3；KK 地下水库蓄量常数，s；Δt 计算时段，s。

地下水库平均入流量 IgI_g 就是地下净雨对地下水库的补给量，即:

Ig=0.278∗R∗FΔt I_g = \frac{0.278 * R * F}{\Delta t}

式中，RR 本时段地下水库净雨量，mm；FF 流域面积，km2。

Q2=F∗R3.6∗(K+0.5Δt)+K−0.5ΔtK+0.5ΔtQ1 Q_2 = \frac{F * R}{3.6 * (K + 0.5 \Delta t)} + \frac{K - 0.5 \Delta t}{K + 0.5 \Delta t} Q_1

Q2=(1−Kg)UR+KgQ1 Q_2 = (1 - K_g) U R + K_g Q_1

其中，KgK_g 为退水系数，U 为流量转换系数。

流量系数模型

通过流量系数模型，将流域产流转为径流量：

Q=U∗R,U=area/(3.6∗dt) Q = U * R, U = area / (3.6 * dt)

其中，area 为流域面积，km2；dt 为计算步长，hour。

单位线模型

单位线（unit hydrograph）又称单位过程线。利用单位线来推求洪水汇流过程线，称单位线法。 单位时段内给定流域上、时空分布均匀的一次单位净雨量在流域出口断面所形成的地面径流(直接径流)过程线。

单位线模型认为给定流域的地面径流 (直接径流) 过程线的形状反映了该流域所有物理特征的影响； 它包括三个基本假定，如在给定时段内和流域面积上净雨量分布均匀。单位线的基本假定为：

1、单位时段内净雨量不同， 但所形成的地面径流过程线的总历时(即底宽)不变；

2、单位时段内n倍单位净雨量所形成的出流过程，其流量值为单位线的n倍；

3、各单位时段净雨所产生的出流过程不相干扰，出口断面的流量等于各单位时段净雨所形成的流量之和。

概言之，上述单位线概念和假定，就是将流域视为集总的线性时不变系统，适用倍比和迭加原则。

单位线是一种由净雨过程推求洪水过程的方法，在设计洪水和水文预报中广泛应用。 控制单位线形状特征的主要指标有：洪峰流量（qm）、洪峰滞时（Tp）和总历时T，合称单位线三要素。 图中坐标h为净雨，q为流量，t为时间、△t为单位时段。

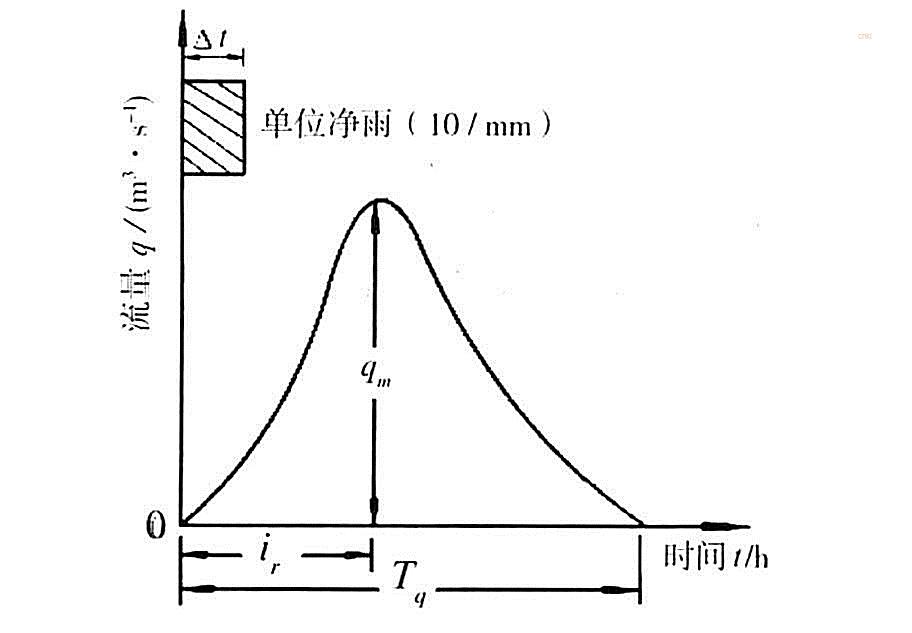
由于单位线的基本假定与实际情况并不完全相符，降雨的时空分布不均，非线性影响和基流分割误差， 使各次洪水所分析的单位线不同，或者出现跳动现象，宜加约束条件或考虑非线性改正。

或简单地依净雨量大小采用分级单位线，对于暴雨地区分布不同则采用分区的单位线。

单位线的时段转换

模型内置了单位线时段转换功能，即应用S—过程线(它是单位线流量的累积曲线)，将两条相同的S—曲线沿时间坐标轴按所需时段平移错开，两曲线间纵标之差乘以时段换算系数，就得所需要的时段单位线。

地貌单位线模型

瞬时单位线是指在无穷小历时的瞬间，输入总水量为1且在流域上分布均匀的单位净雨所形成的流域出流过程线。

纳希（J．E．Nash）1957年提出一个假设，即流域对地面净雨的调蓄作用，可用n个串联的线性水库的调节作用来模拟，由此推导出纳希瞬时单位线的数学方程式：

U(0,t)=1KΓ(n)(tK)n−1etK U(0, t) = \frac{1}{K \Gamma(n)} (\frac{t}{K})^{n-1} e^{\frac{t}{K}}

式中，n 线性水库的个数；K 线性水库的蓄量常数。

纳希用n个串联的线性水库模拟流域的调蓄作用只是一种概念，与实际是有差别的，但导出的瞬时单位线的数学方程式具有实用意义，得到广泛的应用。在实用中，纳希瞬时单位线的n和K并非是原有的物理含义，而是起着汇流参数的作用，n的取值也可以不是整数。n、K对瞬时单位线形状的影响是相似的，当n、K减小时，u(0, t) 的峰值增高，峰现时间提前；而当n、K增大时，u(0, t) 的峰值降低，峰现时间推后。

R.Rosso以将 Nash 模型和基于 Horton-Strahler 河道分级法的地貌参数结合起来，得到用霍顿地貌参数以及河长，流域面积等地形参数共同表达的地貌瞬时单位线。霍顿三大定律分别为河长定律、河数定律和面积定律，与之相应的三个比值为河长比($R_L$)、分叉比($R_B$)和面积比($R_A$)。通常,$R_L$值范围在1.5~3.5, $R_B$值范围在 2.5~5.0，$R_A$值范围在 3.0~6.0。

通过上述地貌参数可利用如下方法计算地貌瞬时单位线:

GIUH(t)=tka−ae−tkkγ(a) GIUH(t) = \frac{t}{k}^{a - a} \frac{e^{\frac{-t}{k}}}{k \gamma (a)}

a=3.29(RBRA)0.78RL0.07，k=0.70(RARBRL)0.48Tc，Tc=LΩv a = 3.29(\frac{R_B}{R_A})^{0.78} {R_L}^{0.07}， k = 0.70(\frac{R_A}{R_B R_L})^{0.48} T_c， T_c = \frac{L_{\Omega}}{v}

地貌瞬时单位线便于对参数进行分析和地区综合，较为适合于中小流域地面径流的汇流计算。

无因次单位线模型

通过无因次单位线实现产流的时程分配。时程分配涉及横向和纵向：

横向时程分配

为方便理解，先作图如下。其中 Tc 地表径流汇流时间，Tp峰值汇流时间；Tb地下径流的汇流时间。

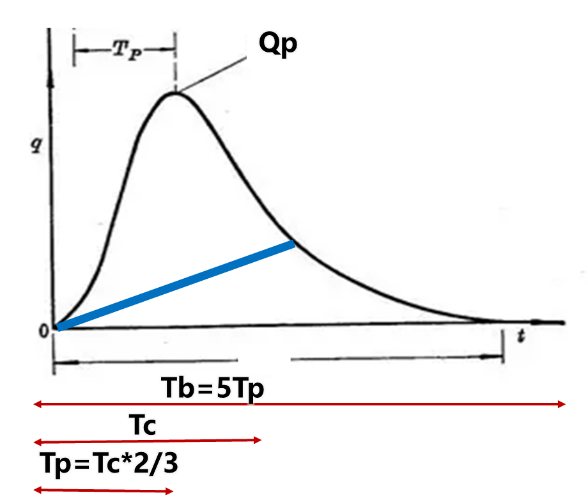
由图可知：只需要求出Tc就可以计算完整的横向时程分配，Tc的单位采用分钟，方便用于城区小区域计算（汇流时间一般不到60分钟），以及大流域计算（一般超过60分钟），所以先采用分钟计算，最后再按照计算时间步长输出结果。

纵向比例分配

按照 Tp 划分的各个时长的比例分配。

Time Ratios Discharge Ratios Mass Curve Ratios
t/Tp q/qp Qa/Q
0 0.000 0.000
0.1 0.030 0.001
0.2 0.100 0.006
0.3 0.190 0.012
0.4 0.310 0.035
0.5 0.470 0.065
0.6 0.660 0.107
0.7 0.820 0.163
0.8 0.930 0.228
0.9 0.990 0.300
1.0 1.000 0.375
1.1 0.990 0.450
1.2 0.930 0.522
1.3 0.860 0.589
1.4 0.780 0.650
1.5 0.680 0.700
1.6 0.560 0.751
1.7 0.460 0.790
1.8 0.390 0.822
1.9 0.330 0.849
2.0 0.280 0.871
2.2 0.207 0.908
2.4 0.147 0.934
2.6 0.107 0.953
2.8 0.077 0.967
3.0 0.055 0.977
3.2 0.040 0.984
3.4 0.029 0.989
3.6 0.021 0.993
3.8 0.015 0.995
4.0 0.011 0.997
4.5 0.005 0.999
5.0 0.000 1.000

浙江水文手册推理公式模型

对于 50 平方公里以下的小流域汇流计算，采用浙江水文手册推理公式模型。

Q=0.278∗area∗hr/τn Q = 0.278 * area * h_r / {\tau}^n

式中，area 为流域面积，km2；h_r 为汇流时间，hour；n 为暴雨衰减指数，一般为0.4142 ~ 0.4831。