一维河网模型（有限差分方法）

0. 前言

​GRMS 一维河网模型采用有限体积方法求解 Saint-Venant（圣维南）方程组，此处进行有限差分方法的求解说明，以供参考。

1. 一维河网基本方程

1.1. 控制方程

​描述天然河网一维浅水流动的 Saint-Venant 方程组，包括连续性方程和动量方程：

B∂Z∂t+∂Q∂x=q∂Q∂t+∂∂x(βuQ)=−gA∂Z∂x−g∣Q∣Qc2AR(1.1) B\frac{\partial Z}{\partial t} + \frac{\partial Q }{\partial x} = q \\ \frac{\partial Q}{\partial t}+\frac{\partial}{\partial x}(\beta u Q)=-gA \frac{\partial Z}{\partial x} - g\frac{|Q| Q}{c^2AR} \tag{1.1} 式中：xx为里程（m）；tt为时间（s）；ZZ为水位（m）；BB为过水断面宽度（m）；QQ为流量（m3/s\text m^3/\text s）；qq为侧向单宽流量（m2/s\text m^2/\text s）；AA为过水断面面积（m2\text m^2）；gg为重力加速度（m/s2\text m/\text s^2）；uu为断面平均流速（m/s\text m/\text s）；β\beta为校正系数；RR为水力半径（m）；cc为谢才系数，c=R1/6nc=\frac{R^{1/6}}{n}，nn为曼宁糙率系数。

1.2. 汊点连接方程

​河网的汊点是相关支流汇入或流出点，汊点处的水流情况通常较复杂，目前对河网进行非恒定流计算时，通常使用近似处理方法，即汊点处各支流水流要同时满足流量衔接条件和动力衔接条件：

流量衔接条件： ∑k=1mQi+q=dVdt=A(Z)dZdt(1.2) \sum_{k=1}^{m} Q_i+ q =\frac{dV}{dt}=A(Z)\frac{dZ}{dt} \tag{1.2} 动力衔接条件： Z1=Z2=...=Zm(1.3) Z_1=Z_2=...=Z_m \tag{1.3} 式中：QiQ_i为汊点第ii条支流流量，流入为正，流出为负；qq为该汊点处的点源；VV为汊点处的蓄水量，AA为汊点蓄水面积，当汊点无蓄水能力时，式(1.2)右端项为0；tt为时间；ZiZ_i表示汊点第条支流的断面平均水位；mm为汊点处的支流数量。

2. 数值格式

​一维河网水流数学模型计算采用“分级联解法”。“分级联解法”的本质是利用河段离散方程的递推关系，建立汊点的离散方程并求解，其算法基本原理为：首先将河段内相邻两断面之间的每一微段上的圣维南方程组离散为断面水位和流量的线性方程组；通过河段内相邻断面水位与流量的线性关系和线性方程组的自消元，形成河段首末断面以水位和流量为状态变量的河段方程；再利用汊点相容方程和边界方程，消去河段首、末断面的某一个状态变量，形成节点水位（或流量）的节点方程组；最后对简化后的方程组采用追赶法求解。

2.1. Preissmann 隐式差分格式

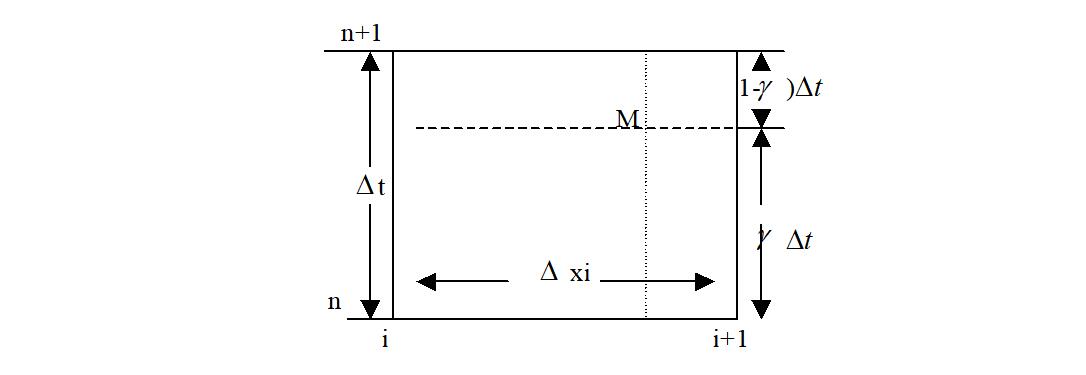
​采用 Preissmann 隐式四点偏心格式差分格点的布置，如图2.1所示。

图2.1 四点隐式差分格式示意图

针对图中的M点建立差分格式，则任意函数及其偏导数的离散形式为：
Fm=12[γ(Fin+1+Fi+1n+1)+(1−γ)(Fin+Fi+1n)](2.1) F_m = \frac 1 2 [\gamma(F_i^{n+1}+F_{i+1}^{n+1})+(1-\gamma)(F_i^n+F_{i+1}^n)] \tag{2.1}

∂F∂t=12Δt[(Fin+1+Fi+1n+1)−(Fin+Fi+1n)](2.2) \frac{\partial F}{\partial t} = \frac{1}{2\Delta t} [(F_i^{n+1}+F_{i+1}^{n+1})-(F_i^{n}+F_{i+1}^{n})] \tag{2.2}

∂F∂x=1Δxi[γ(Fi+1n+1−Fin+1)+(1−γ)(Fi+1n−Fin)](2.3) \frac{\partial F}{\partial x} = \frac{1}{\Delta x_i} [\gamma(F_{i+1}^{n+1}-F_{i}^{n+1})+(1-\gamma )(F_{i+1}^{n}-F_{i}^{n})] \tag{2.3}

式中：ii为断面编号；nn为时间步；Δt\Delta t为计算时间步长；Δx\Delta x为断面间距；γ\gamma为差分系数，0.5<γ<10.5<\gamma<1。

​现考虑由NN个断面组成的单一河道。采用 Preissmann 隐式四点偏心格式离散控制方程各项，可得：
∂Z∂t=12Δt[(Zin+1+Zi+1n+1)−(Zin+Zi+1n)](2.4) \frac{\partial Z}{\partial t} =\frac{1}{2\Delta t}[(Z_i^{n+1}+Z_{i+1}^{n+1})-(Z_i^n+Z_{i+1}^n)] \tag{2.4}

∂Q∂x=1Δxi[γ(Qi+1n+1−Qin+1)+(1−γ)(Qi+1n−Qin)](2.5) \frac{\partial Q}{\partial x} =\frac{1}{ \Delta x_i}[\gamma (Q_{i+1}^{n+1}-Q_{i }^{n+1})+(1-\gamma)(Q_{i+1}^n-Q_{i}^n)] \tag{2.5}

∂Q∂t=12Δt[(Qin+1+Qi+1n+1)−(Qin+Qi+1n)](2.6) \frac{\partial Q}{\partial t} =\frac{1}{2\Delta t}[(Q_{i}^{n+1}+Q_{i+1 }^{n+1})- (Q_{i}^n+Q_{i+1}^n)] \tag{2.6}

∂Z∂x=1Δxi[γ(Zi+1n+1−Zin+1)+(1−γ)(Zi+1n−Zin)](2.7) \frac{\partial Z}{\partial x} =\frac{1}{ \Delta x_i}[\gamma (Z_{i+1}^{n+1}-Z_{i }^{n+1})+(1-\gamma)(Z_{i+1}^n-Z_{i}^n)] \tag{2.7}

∂∂x(βuQ)=1Δxi[γ(βi+1nui+1nQi+1n+1−βinuinQin+1)+(1−γ)(βi+1nui+1nQi+1n−βinuinQin)](2.8) \frac{\partial }{\partial x}(\beta u Q) =\frac{1}{ \Delta x_i}[\gamma (\beta_{i+1}^{n}u_{i+1}^{n}Q_{i+1}^{n+1} -\beta_{i}^{n}u_{i}^{n}Q_{i}^{n+1}) \\ +(1-\gamma)(\beta_{i+1}^{n}u_{i+1}^{n}Q_{i+1}^{n} -\beta_{i}^{n}u_{i}^{n}Q_{i}^{n})] \tag{2.8}

g∣Q∣Qc2AR=(g∣u∣2c2R)inQin+1+(g∣u∣2c2R)i+1nQi+1n+1(2.9) g \frac{|Q|Q}{c^2AR} =(\frac{g|u|}{2c^2R})_i^nQ_{i}^{n+1}+(\frac{g|u|}{2c^2R})_{i+1}^nQ_{i+1}^{n+1} \tag{2.9}

因此，可得圣维南方程组(1.1)的有限差分离散方程：
a1iZin+1−c1iQin+1+a1iZi+1n+1+c1iQi+1n+1=E1i(2.10) a_{1i}Z_{i}^{n+1}-c_{1i}Q_{i}^{n+1}+a_{1i}Z_{i+1}^{n+1}+c_{1i}Q_{i+1}^{n+1}=E_{1i} \tag{2.10}

a2iZin+1−c2iQin+1−a2iZi+1n+1+d2iQi+1n+1=E2i(2.11) a_{2i}Z_{i}^{n+1}-c_{2i}Q_{i}^{n+1}-a_{2i}Z_{i+1}^{n+1}+d_{2i}Q_{i+1}^{n+1}=E_{2i} \tag{2.11}

式中：a1ia_{1i}、c1ic_{1i}、a2ia_{2i}、c2ic_{2i}、d2id_{2i}、E1iE_{1i}、E2iE_{2i}为当前时刻的水位、流量、过水断面面积、水面宽度组成的系数。

2.2. 三级联解

​由2.1可知，若单一河道内首、末断面的水位已知，则河道内所有断面的水位、流量均可求取。因此，河网状态的求解可归结为河网内各河道首、末断面水位的求解。假设河网有N0N_0条河道，N1N_1个边界，N2N_2个汊点，则汊点处的断面数量为2N0−N12N_0-N_1。此时，由动力衔接条件式(1.3)可得2N0−N1−N22N_0-N_1-N_2个等式；由流量衔接条件式(1.2)可得N2N_2个等式。结合N1N_1个边界条件等式，共有2N02N_0个等式。即得到关于河道首、末断面水位的矩阵方程，矩阵维数为2N0×2N02N_0 \times 2N_0。因此，可以求解得到所有河道的首、末断面水位，共计2N02N_0个变量，进而可计算得到河网所有断面的水位、流量。

2.3. 四级联解

由动力衔接条件式(1.3)可知，汊点处各断面的水位相等。与三级联解法中以河网各河道首、末断面的水位为求解变量不同，四级联解法选择各汊点水位作为求解变量。对于具有N2N_2个汊点的河网，由流量衔接条件式(1.2)可得到N2N_2个方程。因此矩阵方程的维数为N2×N2N_2 \times N_2，可求解出N2N_2个汊点的水位。与三级联解法相比，四级联解法的矩阵方程维数较小，计算效率较高。

2.4. 四级联解+压缩矩阵

​当采用四级联解时，以各个汊点的水位为变量建立N2×N2N_2 \times N_2维的方程组进行求解，每个汊点只与与其相连的汊点之间通过河道连接，因此系数矩阵具有较高的稀疏性，如果河网汊点编码比较理想时，系数矩阵具有带状特性，此时采用压缩矩阵的处理技术，节省空间，减少不必要的乘除法计算，可以大大提升计算效率。值得注意的是，三种求解方法的效率并非递增，四级联解的两种方法在河网较复杂时的效率才会体现出来。

2.5. 河流断流的处理

河网区内的某些支汊河段，由于枯水曲干流水位较低，河道高程高于水位，河段出现断流现象，如不做处理，将无法进行计算。GRMS采用半窄缝法处理干河床的演进。“窄缝法”是处理干河床的有效方法之一，在二维问题中应用较多，它假设在干河床处各空间步长内均存在一条窄缝，缝内的水流与干河床相连，其关键是定义窄缝的宽度与修正原始的水流运动方程。根据“窄缝法”的思想，假设在河网区域内存在一条最低点高程较低的窄缝，使得在各种情况下各河段均有水流通过，且其蓄水量对整个河网的水量守恒不产生大的影响。计算过程中如果河道水位高于断面最低点高程时，采用河道正常糙率，若水位低于断面最低点高程时，河道糙率取一较大值，起到阻水作用，抬升断面水位，直至断流状态结束，模拟的这一现象与实际水流运动规律及其相似。在采用此方法时，并没有修正控制方程，不完全满足“窄缝法”的原理，称为“半窄缝法”，在模拟大尺度河网水流运动时，是一种有效的方法。