数值计算方法
采用边界拟合能力强和易于局部网格加密的三角形网格剖分计算域,利用基于水位-体积关系的斜底三角单元模型,有效解决了小尺度线状地形模拟难题;以能够有效捕获激波的 Godunov 型有限体积法为框架,运用在时间上和空间上均具有二阶精度的 MUSCL-Hancock 预测-校正格式离散洪水控制方程,采用 HLLC 近似 Riemann 算子计算对流数值通量,采用直接近似方法计算扩散数值通量,并结合斜率限制器以保证模型的高分辨率特性,避免在间断或大梯度解附近产生非物理虚假振荡;基于单元中心型底坡项近似方法,在不使用任何额外动量通量校正项的前提下模型能保持通量梯度与底坡项之间的平衡,即模型具有和谐性质;采用半隐式格式处理摩阻项,该半隐式格式既能保证不改变流速分量的方向,也能避免小水深引起的非物理大流速问题,有利于计算稳定性;实现了固壁、水位、流量、自由出流等边界条件;基于 CFL 稳定条件实现了数值模型的自适应时间步长技术。
计算网格
鉴于三角形单元具有复杂边界拟合能力强、便于网格生成和局部加密等特点,本模型采用非结构三角形单元作为计算网格,如图3.2-1所示。其中,为待计算单元,其顶点1-顶点2-顶点3排序服从逆时针方向;与顶点相对的边为,其外法向单位向量为;单元的邻接单元中,与顶点相对的单元为。

图1 非结构三角形单元拓扑结构示意图
对于每一个节点而言,其网格拓扑信息包括:节点序号,节点坐标,节点周围的单元;对于每一条边而言,其网格拓扑信息包括:边序号,边的左、右单元,边的始、末节点;对于每一个单元而言,其网格拓扑信息包括:单元序号,单元的三个顶点,单元的三条边,单元的三个邻接单元。在模型开始计算之前,需要根据网格文件构造包含上述拓扑信息的计算网格系统。
斜底三角单元
本模型采用斜底三角单元模型,即将底高程定义于单元顶点处。这种方式在地形表达精度方面为二阶精度。
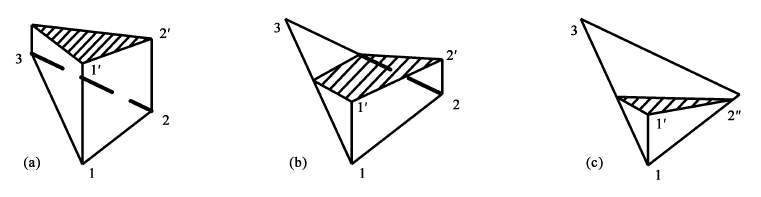
图2 不同水位条件下的斜底单元
模型计算时,水深为守恒变量,表征单元的水量,即 Vi=hiΩi,其中 Vi 为水量。图2中,斜线阴影面为水面,三角形 Δ123 为单元底面,(a)中3个顶点的水深均大于零,(b)和(c)存在水深为零的顶点。假设底高程满足 bin,1⩽bin,2⩽bin,3,基于此,单元水位 zi 与水量存在如下关系:
Vi/Ωi=hi=⎩⎨⎧(zi−bin,1)3/[3(bin,2−bin,1)(bin,3−bin,1)](zi2+zibin,3−3zibin,1−bin,2bin,3+bin,1bin,2+bin,1bin,1)/[3(bin,3−bin,1)](zi−bi)if bin,1<zi⩽bin,2if bin,2<zi⩽bin,3if zi>bin,3(1)
式中 bi 为单元形心处的底高程,bi=(bin,1+bin,2+bin,3)/3⩾bin,1。模型初始化时,若以水位为初始条件,则通过式(1)可计算出单元水深值;模型计算过程中,对单元水深值进行更新后,通过式(1)可计算出相应的单元水位值。与平底单元相比,基于水位~体积关系建立的斜底单元模型,使单元水位的值域由 [bi,+∞) 扩展为 [bin,1,+∞),避免了干湿界面计算时重构干单元底高程,提高了模型的动边界处理能力,有利于设计具有和谐性的计算格式。
有限体积离散
在任意控制体上对式(1)所示的控制方程进行积分得:
∂t∂∫ΩUdΩ+∫Ω(∂x∂Eadv+∂y∂Gadv)dΩ=∫Ω(∂x∂Ediff+∂y∂Gdiff)dΩ+∫ΩSdΩ(2)
根据格林公式,将上式转化为沿其边界的线积分,可得:
∂t∂∫ΩUdΩ+∮∂ΩFadv⋅ndℓ=∮∂ΩFdiff⋅ndℓ+∫ΩSdΩ(3)
式中,∂Ω为控制体Ω的边界;n为边界的外法向单位向量;dΩ、dℓ分别为面积微元和弧微元;Fadv=[Eadv,Gadv];Fdiff=[Ediff,Gdiff]。
在平面二维三角形网格中,线积分可分别由下式计算:
∮∂ΩFadv⋅ndℓ=1∑3Fadv⋅nkLk(4)
∮∂ΩFdiff⋅ndℓ=1∑3Fdiff⋅nkLk(5)
假设Ui为U在单元Ci内的平均值,即:
Ui=Ωi1∫CiUdΩ(6)
则有:
ΩidtdUi=−k=1∑k=3Fi,kadv⋅ni,kLi,k+k=1∑k=3Fi,kdiff⋅ni,kLi,k+Si(7)
式中,Ωi为单元Ci的面积;Fi,kadv 、Fi,kdiff、ni,k、Li,k分别代表单元第条边的对流数值通量、扩散数值通量、外法向单位向量和长度;Si为源项近似。
数值通量计算
由于积分平均,物理变量在每个单元内部为常数,在整个计算域内形成阶梯状分布,因此在单元界面处物理量存在间断,即界面左、右两侧的物理量不相等,故而在界面处构成了一个局部 Riemann 问题。通过 Riemann 问题的求解可得到界面处的对流数值通量,即:
Fadv⋅n=[Eadv,Gadv]⋅[nx,ny]=Eadvnx+Gadvny=⎣⎡h(unx+vny)hu(unx+vny)+21g(h2−b2)nxhv(unx+vny)+21g(h2−b2)ny⎦⎤(8)
令
u⊥=unx+vnyu//=−uny+vnx(9)
式中,u⊥、u//分别为与界面垂直和平行的流速分量;定义:
U^=T(n)⋅U=⎣⎡1000nx−ny0nynx⎦⎤⋅U=⎣⎡hhu⊥hu//⎦⎤(10)
代入(12)可得:
Fadv⋅n=⎣⎡hu⊥huu⊥+21g(h2−b2)nxhvu⊥+21g(h2−b2)ny⎦⎤=⎣⎡1000nxny0−nynx⎦⎤E(U^)(11)
可知,二维浅水方程的对流数值通量计算可转化为界面处一维 Riemann 问题求解。
如图2所示,在平面上,二维浅水方程 Riemann 解中存在三个波,分为三类:激波(shock wave)、稀疏波(rarefaction wave)和接触波(contact wave)。三个波将初始的两个常状态区分割为四个常状态区,其中左、右两个区域的状态分别为初始的左、右状态值,中间两个区域的状态则由 Riemann 解的结构确定。

图2 二维浅水方程的Riemann解结构
本模型采用能够满足熵条件的 HLLC 黎曼求解器计算二维浅水方程的对流数值通量:
Fadv(UL,UR)⋅n=⎩⎨⎧FLadvF∗LadvF∗RadvFRadvif s1⩾0if s1<0⩽s2if s2<0<s3if s3⩽0(12)
式中,FLadv=Fadv(UL)⋅n、FRadv=Fadv(UR)⋅n ,均有式(3.2-15)计算,其中UL、UR分别为局部 Riemann 问题所在边界左侧与右侧的守恒变量;F∗Ladv、F∗Radv分别为局部 Riemann 解中间区域接触波左右侧的数值通量;s1、s2、s3分别为左波、接触波和右波的波速。
F∗Ladv=⎣⎡(EHLLadv)1(EHLLadv)2nx−u//,L(EHLLadv)1ny(EHLLadv)2ny+u//,L(EHLLadv)1nx⎦⎤(13)
F∗Radv=⎣⎡(EHLLadv)1(EHLLadv)2nx−u//,R(EHLLadv)1ny(EHLLadv)2ny+u//,R(EHLLadv)1nx⎦⎤(14)
式中(EHLLadv)1、(EHLLadv)2分别为运用 HLL 格式计算得到的法向数值通量的第一、二个分量:
EHLLadv=s3−s1s3Eadv(U^L)−s1Eadv(U^R)+s1s3((U^R)−(U^L))(15)
本模型采用 Einfeldt 波速近似计算波速:
s1={min(u⊥,L−ghL,u⊥,∗−gh∗)u⊥,R−2ghRif hL>0 if hL=0(16)
s3={min(u⊥,L+ghR,u⊥,∗+gh∗)u⊥,L−2ghLif hR>0 if hR=0(17)
其中h∗、u⊥,∗为 Roe 平均:
h∗=21(hL+hR)(18)
u⊥,∗=hL+hRhLu⊥,L+hRu⊥,R(19)
由于激波的波速小于激波后面区域的特征波速,此时 Einfeldt 波速即为激波速的 Roe 近似,因此使用 Einfeldt 波速可以获得在激波附近更加准确的数值解。接触波波速:
s2=hR(u⊥,R−s3)−hL(u⊥,L−s1)s1hR(u⊥,R−s3)−s3hL(u⊥,L−s1)(20)
扩散数值通量采用下式计算:
Fi,kdiff⋅ni,k=⎣⎡0hi,kνt[2∂x∂u∣i,kni,kx+(∂y∂u+∂x∂v)∣i,kni,ky]hi,kνt[(∂y∂u+∂x∂v)∣i,kni,kx+2∂y∂v∣i,kni,ky]⎦⎤(21)
式中,hi,k为单元Ci第k条边所在界面处的水深;∂x∂u∣i,k、∂y∂u∣i,k、∂x∂v∣i,k、∂y∂v∣i,k为流速分量在单元Ci第k条边所在界面处的斜率。
变量重构和斜率限制函数
如果物理量在单元内近似为常数分布,并且以各单元形心处的值作为界面处局部 Riemann 问题的初始间断条件,则相应的计算格式在空间上仅具有一阶精度,存在较大的数值耗散。对水流模拟而言,一阶精度的计算格式能基本满足工程应用的要求。然而,对泥沙运动或者污染物扩散模拟而言,一阶格式的过度数值耗散往往导致计算结果失真。为了提高格式的空间精度,在构造界面处局部 Riemann 问题时,需要采用比分片常数近似函数更高精度的重构方法对界面左、右两侧的变量进行重构,并基于重构变量求解界面处的数值通量。本模型针对不同的单元干湿状态,采用不同的变量重构方法。
若单元处于局部淹没状态,则采用采用该单元形心处的值为重构值,否则若单元处于全淹状态,则采用线性重构并结合梯度限制器计算水位、流速的重构值:
p(x,y)=pi+∇pi⋅r(22)
式中,p为重构变量,如水位、流速;r为界面中点相对于单元形心处的位置矢量;∇pi为限制梯度:
∇pi=φi∇pi(23)
其中φi为限制函数:
φi=k=1,2,3min(φk) φk=⎩⎨⎧min(1,pi,kRec−pipimax−pi)min(1,pi,kRec−pipimin−pi)1if pi,kRec−pi>0if pi,kRec−pi<0if pi,kRec−pi=0(24)
其中pi,kRec为单元顶点处未受限制的重构值,pimax=maxpi,k,pimin=minpi,k, k=1,2,3。
底坡项近似
在每一个计算步,本模型均对所有单元进行连续方程和动量方程的更新,即同时更新单元的水深和流速。因此,需要对所有单元进行底坡项处理。
若单元为全淹没状态,本模型采用单元中心型近似方法处理底坡项:
Si,0x=−∫C1g(h+b)∂x∂bdΩ=−g(h+b)Ω∂x∂b∣i(25)
否则,本模型采用 DFB(Divergence Form for Bed slope source term)技术处理底坡项:
Si,0x=k=1∑321g(hi,kRec)2Li,kni,kx−k=1∑321g(bi,k)2Li,kni,kx(26)
式中,bi,k为单元Ci第k条边的中点位置底高程。
采用上述底坡项近似方法,保证了模型的和谐性。
摩阻项处理
一般地,摩阻项通过算子分裂法进行处理:
dtdU=Sf(U)⟹dtd⎣⎡hhuhv⎦⎤=⎣⎡0−gn2huu2+v2/h4/3−gn2hvu2+v2/h4/3⎦⎤(27)
单元水深保持不变 式(31)可简化为:
dtd[uv]=−gn2h−4/3[uu2+v2vu2+v2](28)
复杂地形的陡峭坡面,使局部区域的水深较小、流速较大,使得式(3.2-32)对应的常微分方程系统的 Lipschitz 常数很大,因此,摩阻项可能引起刚性问题。此时,若采用一般的显式数值方法处理摩阻项,将显著影响数值计算的稳定性,或将极大减小全局时间步长,从而严重降低计算效率。为解决上述问题,需要采用隐式或半隐式格式处理摩阻项。然而,由于水深变量位于摩阻项的分母,一般的隐式或半隐式计算格式仍面临一些问题,如产生错误的大流速、改变流速分量的方向等。
综合考虑摩阻项处理的稳定性和计算效率,本模型采用如下半隐式格式处理摩阻项:
Δtun+1−un=(−gn2u2+v2h−4/3)∣nun+1(29)
柯氏力项处理
与魔阻项类似,柯氏力项通过算子分裂法进行处理:
∂t∂U=Sk(U)⟹∂t∂⎣⎡hhuhv⎦⎤=⎣⎡0fhv−fhu⎦⎤(30)
由于在柯氏力项处理过程中, 式(34)可简化为:
∂t∂[uv]=[fv−fu](31)
采用如下隐式差分格式:
Δtun+1−un=fnvn+1Δtvn+1−vn=fnun+1(32)
时间二阶积分
在二维浅水方程数值求解过程中,时间上离散可采用 Runge-Kutta、Hancock 预测-校正等多步格式,以提高模型的时间精度。从计算效率看,在一个时间步长内,两步 Runge-Kutta 法分别对所有单元界面计算两次黎曼问题,而 Hancock 预测-校正法只需要计算一次黎曼问题,因此,Hancock 预测-校正法的计算效率相对较高;从格式稳定性看,Runge-Kutta 法可满足 TVD 性质,而 MUSCL-Hancock 法在合理选择时间步长的前提下满足 L1 稳定。考虑模型的计算效率,本模型采用 Hancock 预测-校正格式实现二维浅水方程数值求解的时间二阶积分。
(1)预测步
在预测步,计算域的水流状态由t时刻更新至t+21Δt时刻,其中Δt为计算时间步长。Δt可以设定为常数,也可以根据稳定条件进行自适应调整。预测步不考虑紊动扩散项。
若单元为全干或局部淹没状态,则以当前时刻的水位、流速作为预测步的结果;若单元为全淹没状态,则以水位、流速作为预测变量:
ηit+Δt/2=ηit2Δt(h∂xu+h∂yv+u∂xh+v∂yh)∣it(33)
uit+Δt/2=1+gn2h−4/3u2+v2Δt/21[u−2Δt(u∂xu+g∂xη+v∂yu)]∣it(34)
vit+Δt/2=1+gn2h−4/3u2+v2Δt/21[v−2Δt(u∂xv+g∂yη+v∂yv)]∣it(35)
由于静水条件下流速为零、水位为常数,因此,由式(3.2-33)~(3.2-35)可知,预测步的水流静止状态得以维持。
(2)校正步
在校正步,计算域的水流状态由t时刻更新至t+Δt时刻。基于守恒形式浅水方程,由下式对单元值进行更新:
Uit+Δt=Uit+ΩiΔt[k=1∑3(−Fi,kadv+Fi,kdiff)⋅ni,kℓi,k+Si]t+Δt/2(36)
边界条件
一般情况下,模型的边界条件实现方式有两种:镜像单元法和直接计算数值通量法。其中,前者在基于结构网格的数学模型中应用较广,而后者被广泛运用于基于非结构网格的数值模型。本模型采用直接计算数值通量的方式实现边界条件。
边界处的对流数值通量为:
Fadv⋅n=⎣⎡h∗U⊥,∗h∗u∗u⊥,∗+21g(h∗2−b2)nxh∗v∗u⊥,∗+21g(h∗2−b2)ny⎦⎤(37)
式中,h∗、u∗、u⊥,∗分别代表边界边中点处的水深、x方向流速分量、界面外法向方向流速分量;b为边界边中点处的底高程值;nx、ny为分别为边界边的外法向单位向量在x和y方向分量。
由式(37)可知,计算边界边对流数值通量的关键在于估算边界边中点处的水深、流速等物理量。
(1)急流开边界条件
由浅水方程特征理论可知,水流为急流状态时信息沿下游传播,因此急流出口边界的扰动不会对计算域内的水流状态产生影响。故急流边界处的水深、流速等水力要素值采用边界边所在内单元的水力要素值:
h∗=hL(38)
u∗=uL, v∗=vL(39)
在数值模拟中,常采用自由出流边界条件,其实现方式与急流开边界条件相同。
(2)缓流开边界条件
假设边界边的左侧位于计算域之内、右侧位于计算域之外,基于浅水方程特征理论,由一维浅水方程的 Riemann 不变量可得:
u⊥,∗+2gh∗=u⊥,L+2ghL(40)
式中,hL、u⊥,L分别为边界边所在内单元形心处的水深和界面外法向方向流速分量。
式(40)中存在两个未知变量,因此需要结合边界条件建立关于h∗与u⊥,∗的等式,进而通过求解方程组计算和。
对于水位边界,可根据水位求出边界上的水深h∗,从而可以求出流速u⊥,∗;对于流量边界,可求出边界边的单宽流量q⊥,∗,从而求出h∗与u⊥,∗的一个关系式:q⊥,∗=h∗u⊥,∗,结合式(3.2-44)可以求出h∗与u⊥,∗;对于固壁边界,即边界上的法向流速为零,且假设边界上的水深等于边界边所在单元形心处的水深值,即u⊥,∗=0.0, h∗=hL。
稳定条件
为保持显示格式的稳定,通常采用 CFL 稳定性条件限制时间步长Δt:
Δt=Cr⋅i,kmin[((∣u⊥∣+gh)LkΩ)i],i=1,2,⋯,N;k=1,2,3(41)
式中,Δt为 Courant 数,0<Cr<1,u⊥和h为界面的 Roe 平均;N为计算网格单元的个数。


